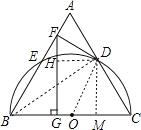
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为 .

参考答案:
【答案】3![]()
【解析】
试题分析:连结OD,作DH⊥FG于H,DM⊥BC于M,根据等边三角形的性质得∠A=∠C=∠ABC=60°,AC=BC,根据切线的性质得OD⊥DF,再证明OD∥AB,则DF⊥AB,在Rt△ADF中根据含30度的直角三角形三边的关系得DF=![]() AF=2
AF=2![]() ,由BC为⊙O的直径,根据圆周角定理得∠BDC=90°,则AD=CD=4,OD=4,所以OM=
,由BC为⊙O的直径,根据圆周角定理得∠BDC=90°,则AD=CD=4,OD=4,所以OM=![]() OD=2,在Rt△DFH中可计算出FH=
OD=2,在Rt△DFH中可计算出FH=![]() ,DH=
,DH=![]() FH=3,则GM=3,于是OG=GM﹣OM=1,BG=OB﹣OG=3,在Rt△BGF中可计算FG=
FH=3,则GM=3,于是OG=GM﹣OM=1,BG=OB﹣OG=3,在Rt△BGF中可计算FG=![]() BG=3
BG=3![]() .
.
解:连结OD,作DH⊥FG于H,DM⊥BC于M,如图,
∵△ABC为等边三角形,
∴∠A=∠C=∠ABC=60°,AC=BC,
∵DF是圆的切线,
∴OD⊥DF,
∵△ODC为等边三角形,
∴∠ODC=60°,
∴∠A=∠ODC,
∴OD∥AB,
∴DF⊥AB,
在Rt△ADF中,AF=2,∠A=60°,
∴AD=4,DF=![]() AF=2
AF=2![]() ,
,
∵BC为⊙O的直径,
∴∠BDC=90°,
∴BD⊥AC,
∴AD=CD=4,
∴OD=4,
∴OM=![]() OD=2,
OD=2,
在Rt△DFH中,∠DFH=60°,DF=2![]() ,
,
∴FH=![]() ,DH=
,DH=![]() FH=3,
FH=3,
∴GM=3,
∴OG=GM﹣OM=1,
∴BG=OB﹣OG=3,
在Rt△BGF中,∠FBG=60°,BG=3,
∴FG=![]() BG=3
BG=3![]() .
.
故答案为3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2016的值为( )
A.﹣1007 B.﹣1008 C.﹣1009 D.﹣1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和与外角和的总和为1800°,求这个多边形的边数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
A.众数 B.中位数 C.平均数 D.极差
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A=(2+1)(22+1)(24+1)(28+1),则A的末位数字是( ).
A. 4 B. 5 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为 .(
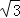 ≈1.7)
≈1.7)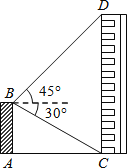
-
科目: 来源: 题型:
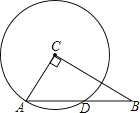
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A.
 B.
B.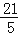 C.
C. D.
D.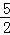
相关试题

