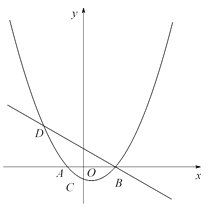
【题目】如图,已知抛物线![]() (a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线
(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线![]() 与抛物线的另一交点为D,且点D的横坐标为﹣5.
与抛物线的另一交点为D,且点D的横坐标为﹣5.
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB, 求△PBD面积的最大值.
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当F坐标为(-2,
;(3)当F坐标为(-2, ![]() )时,点M在整个运动过程中用时最少.
)时,点M在整个运动过程中用时最少.
【解析】试题分析: (1)首先求出点A、B坐标,然后求得点D坐标,代入抛物线y=a(x+2)(x-4)(a为常数,且a>0),求得抛物线解析式;
(2) 设P(m, ![]() ),根据三角形的面积公式即可得解;
),根据三角形的面积公式即可得解;
(3)由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+![]() DF.作辅助线,将AF+
DF.作辅助线,将AF+![]() DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
试题解析:(1)抛物线![]() 令y=0,解得x=-2或x=4,
令y=0,解得x=-2或x=4,
∴A(-2,0),B(4,0).
∵直线![]() 经过点B(4,0),
经过点B(4,0),
∴![]() ,解得
,解得![]() ,
,
∴直线BD解析式为: ![]() .
.
当x=-5时,y=3![]() ,
,
∴D(-5,3![]() ).
).
∵点D(-5, ![]() )在抛物线
)在抛物线![]() 上,
上,
∴![]() ,
,
∴![]() .
.
∴抛物线的函数表达式为: ![]() .
.
(2)设P(m, ![]() )
)
∴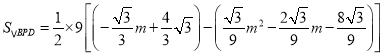
![]() .
. ![]()
∴△BPD面积的最大值为![]() ..
..
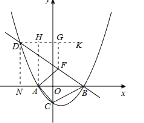
(3)作DK∥AB,AH⊥DK,AH交直线BD于点F,
∵由(2)得,DN=![]() ,BN=9,容易得∠DBA=30°,∴∠BDH=30°,
,BN=9,容易得∠DBA=30°,∴∠BDH=30°,
∴FG=DF×sin30°=![]() ,
,
∴当且仅当AH⊥DK时,AF+FH最小,
点M在整个运动中用时为:t=![]() ,
,
∵lBD: ![]() ,∴Fx=Ax=-2,F(-2,
,∴Fx=Ax=-2,F(-2, ![]() )
)
∴当F坐标为(-2, ![]() )时,用时最少.
)时,用时最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列结论:(1)三点确定一个圆;(2)弧的度数指弧所对圆周角的度数;(3)三角形的内心是三边中垂线交点,它到三角形各边的距离相等;(4)同圆或等圆中,弦相等则弦所对的弧相等。其中正确的个数有( )
A. 0B. 1C. 3D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:写出二元一次方程x﹣3y=6的几个解:
 ,
,  ,
,  ,…,发现这些解的一般形式可表示为
,…,发现这些解的一般形式可表示为  (m为有理数).把一般形式再变形为
(m为有理数).把一般形式再变形为  ,可得
,可得  =y+2,整理得原方程x﹣3y=6.根据阅读材料解答下列问题:若二元一次方程ax+by=c的解,可以写成
=y+2,整理得原方程x﹣3y=6.根据阅读材料解答下列问题:若二元一次方程ax+by=c的解,可以写成  (n为有理数),则a+b+c= .
(n为有理数),则a+b+c= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于点H.
(1)若E是BC的中点,求证:DE=CF;
(2)若∠CDE=30°,求
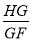 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为
 的中点,BE⊥CD垂足为E.
的中点,BE⊥CD垂足为E.
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB=
 ,求OE的长度.
,求OE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,若∠A∶∠B=1∶5,则∠D=_______;若∠A+∠C=140°,则∠D=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用长度为8cm,9cm,10cm的三条线段_______构成三角形.(填“能”或“不能”)
相关试题

