【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.请你判定四边形BMDN是什么特殊四边形,并说明理由. 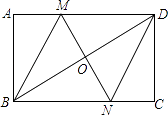
参考答案:
【答案】解:四边形BMDN是菱形.理由如下: ∵四边形ABCD是矩形,
∴AD∥BC,OD=OB,
∴∠MDO=∠NBO,
∵MN是BD的垂直平分线
∴在△MOD与△NOB中, ,
,
∴△MOD≌△NOB(ASA),
∴MO=NO,
∴四边形BMDN是平行四边形.
∵MN是BD的垂直平分线,
∴平行四边形BMDN是菱形.
【解析】根据全等三角形的判定定理ASA证得△MOD≌△NOB,则由全等三角形的对应边相等推知MO=NO,所以“对角线互相平分的四边形BMDN是平行四边形,然后由”对角线互相垂直平分的平行四边形是菱形“证得结论﹣﹣四边形BMDN是菱形. ∴∠MOD=∠NOB=90°.
【考点精析】根据题目的已知条件,利用菱形的判定方法和矩形的性质的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每一个外角都是40°,则这个多边形是( )
A. 六边形 B. 八边形 C. 九边形 D. 十边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】用两种方法证明“三角形的外角和等于360°”.
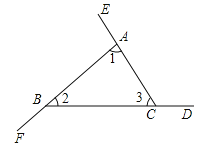
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2的小正方形和边长为x的大正方形放在一起.

(1)用x表示阴影部分的面积;
(2)计算当x=5时,阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法请分别做出判断,并证明.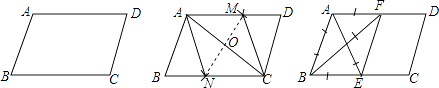
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初一(二)班5位教师决定带领本班a名学生在五一期间在元旦期间去珠海长隆海洋王国旅游,每张票的价格为350元,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律六折优惠.
(1)分别用代数式表示参加这两家旅行社所需的费用;
A旅行社所需费用为 元,B旅行社所需费用为 元,
(2)如果这5位教师要带领该班30名学生参加旅游,你认为选择哪一家旅行社较为合算,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)
(1)求出两个动点运动的速度;
(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;
(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.
相关试题

