【题目】问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题
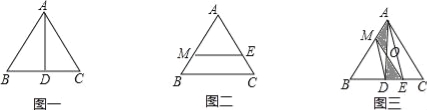
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE.
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
参考答案:
【答案】(1)AD=![]() ;(2)ME=
;(2)ME=![]() ;(3)详见解析;(3)
;(3)详见解析;(3)![]() ≤l≤
≤l≤![]() .
.
【解析】
试题分析:(1)根据等腰三角形三线合一即可证明,利用直角三角形30°性质,即可求出AD.(2)根据相似三角形性质面积比等于相似比的平方,即可解决问题.(3)如图三中,作MN⊥AE于N,DF⊥AE于F,先证明MN=DF,推出四边形MNFD是平行四边形即可.
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,求出EM,利用不等式性质证明ME≥![]() 即可解决问题.
即可解决问题.
试题解析:(1)如图一中,
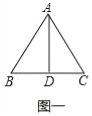
∵AB=AC=BC=2,AD⊥BC,
∴BD=DC,
∴S△ABD=S△ADC,
∴线段AD是△ABC的面径.
∵∠B=60°,
∴sin60°=![]() ,
,
∴![]() ,
,
∴AD=![]() .
.
(2)如图二中,
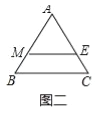
∵ME∥BC,且ME是△ABC的一条面径,
∴△AME∽△ABC,![]() =
=![]() ,
,
∴![]() ,
,
∴ME=![]() .
.
(3)如图三中,作MN⊥AE于N,DF⊥AE于F.
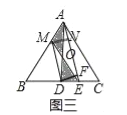
∵S△MOA=S△DOE,
∴S△AEM=S△AED,
∴![]() AEMN=
AEMN=![]() AEDF,
AEDF,
∴MN=DF,
∵MN∥DF,
∴四边形MNFD是平行四边形,
∴DM∥AE.
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,
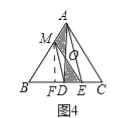
∵DM∥AE,
∴![]() ,
,
∴![]() ,
,
∴xy=2,
在RT△MBF中,∵∠MFB=90°,∠B=60°,BM=x,
∴BF=![]() x,MF=
x,MF=![]() x,
x,
∴ME=![]()
∴ME≥![]() ,
,
∵ME是等边三角形面径,AD也是等边三角形面积径,
∴等边三角形ABC的面径长l的取值范围![]() ≤l≤
≤l≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设M=(x-3)(x-7),N=(x-2)(x-8),则M与N的关系为( )
A.M<N
B.M>N
C.M=N
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】在频数分布直方图中,各个小组的频数比为1∶5∶4∶6,则对应的小长方形的高的比为( )
A. 1∶4∶5∶3 B. 1∶5∶3∶6
C. 1∶5∶4∶6 D. 6∶4∶5∶1
-
科目: 来源: 题型:
查看答案和解析>>【题目】二孩子政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度,在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:
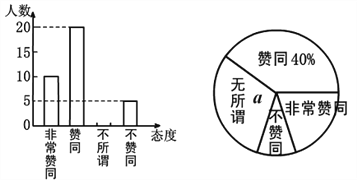
(1)在这次问卷调查中一共抽取了__________名学生,a=________%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
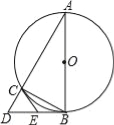
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初中学生在家做家务情况,随机抽取了该校部分初中生进行调查,依据相关数据绘制成以下不完整的统计图.
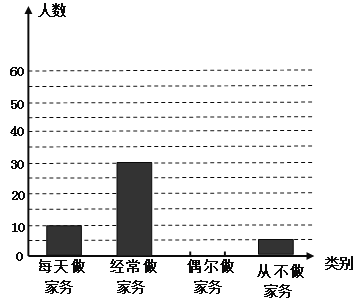
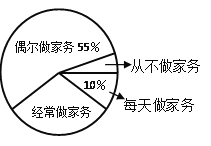
根据以上信息解答下列问题:
(1)此次调查该校抽取的初中生人数 名,“从不做家务”部分对应的扇形的圆心角度数为 ;
(2)补全条形统计图;
(3)请估计该校2000名初中生中“经常做家务”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下问题,不适合用普查的是( )
A. 了解全班同学每周阅读的时间B. 亚航客机飞行前的安全检测
C. 了解全市中小学生每天的零花钱D. 某企业招聘部门经理,对应聘人员面试
相关试题

