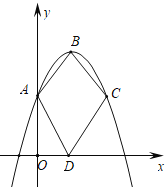
【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+2与y轴交于点A，点B是抛物线的顶点，点C与点A是抛物线上关于对称轴对称的两个点，点D在x轴上运动，则四边形ABCD的两条对角线的长度之和的最小值为_____．

【答案】

【解析】

先将函数化为顶点式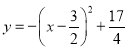，所以顶点坐标，对称轴为直线，BD最小值为，又点C与点A是抛物线上的两个对称点，对称轴为直线，所以C（3，2），AC＝3，因此四边形ABCD的两条对角线的长度之和AC+BD的最小值为．

解：∵y＝﹣x2+3x+2＝，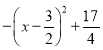

∴，对称轴为直线

∴当BD⊥x轴时，BD最小，BD＝

令x＝0，则y＝2，

∵C与点A是抛物线上关于对称轴对称的两个点，对称轴为直线，

∴C（3，2）

∴AC＝3，

四边形ABCD的两条对角线的长度之和AC+BD的最小值为，

故答案为．

关闭