【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为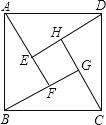
参考答案:
【答案】![]()
【解析】解:设小正方形EFGH面积是a2 , 则大正方形ABCD的面积是13a2 , ∴小正方形EFGH边长是a,则大正方形ABCD的面积是 ![]() a,
a,
∵图中的四个直角三角形是全等的,
∴AE=DH,
设AE=DH=x,
在Rt△AED中,AD2=AE2+DE2 ,
即13a2=x2+(x+a)2
解得:x1=2a,x2=﹣3a(舍去),
∴AE=2a,DE=3a,
∴tan∠ADE= ![]() ,故答案为:
,故答案为: ![]() .
.
小正方形EFGH面积是a2 , 则大正方形ABCD的面积是13a2 , 则小正方形EFGH边长是a,则大正方形ABCD的面积是 ![]() a,设AE=DH=x,利用勾股定理求出x,最后利用熟记函数即可解答.此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边,进一步运用锐角三角函数的定义求解.
a,设AE=DH=x,利用勾股定理求出x,最后利用熟记函数即可解答.此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边,进一步运用锐角三角函数的定义求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
-
科目: 来源: 题型:
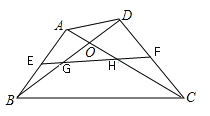
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别相交是AB、CD的中点,EF分别交BD、AC于点G、H。求证:OG=OH。
-
科目: 来源: 题型:
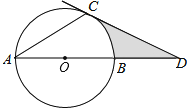
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
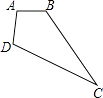
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

相关试题

