【题目】已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
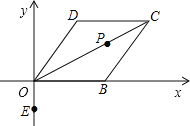
(1)点D的坐标为 ,点C的坐标为 ;
(2)若点P是对角线OC上一动点,点E(0,﹣![]() ),求PE+PB的最小值.
),求PE+PB的最小值.
参考答案:
【答案】(1)(1,![]() ),(3,
),(3,![]() );
);
(2)![]() .
.
【解析】
试题分析:(1)作DF⊥OB于点F,在直角△ODF中利用三角函数求得DF和OF的长,则D的坐标即可求得,然后根据CD∥OB,则C的坐标即可求得;
(2)B关于OC的对称点是D,则DE的长就是PE+PB的最小值,作DH⊥y轴于点H,首先在直角△OGH中利用勾股定理求得DH和OH的长,然后在直角△HED中利用勾股定理求解.
解:(1)作DF⊥OB于点F.
∵B的坐标是(2,0),
∴OB=2,
∴菱形OBCD中,OD=OB=CD=2,
在直角△ODF中,DF=ODsin∠DOB=2×![]() =
=![]() ,OF=ODcos∠DOB=2×
,OF=ODcos∠DOB=2×![]() =1,
=1,
则D的坐标是(1,![]() ).
).
则C的坐标是(3,![]() ).
).
故答案是:(1,![]() ),(3,
),(3,![]() );
);
(2)作DH⊥x轴于点H,连接DE.
在直角△OGH中,∠HOG=90°﹣∠DOB=90°﹣60°=30°.
GH=ODsin∠HOG=2×![]() =1,OH=OGcos∠HOG=2×
=1,OH=OGcos∠HOG=2×![]() =
=![]() .
.
则HE=2![]() .
.
在直角△HEG中,DE=![]() =
=![]() =
=![]() .
.
即PE+PB的最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次体育达标测试中,小明所在小组的六位同学的立定跳远成绩如下(单位:m):2.00,2.11,2.21,2.15,2.20,2.17,那么这组数据的中位数是( ).
A.2.16 B.2.15 C.2.14 D.2.13
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一列不全为零的数除了第一个数和最后一个数外,每个数都等于前后与它相邻的两数之和,则称这列数具有“波动性质”.已知一列数共有2016个,且具有“波动性质”,则这2016个数的和为( )
A.﹣64 B.0 C.18 D.64
-
科目: 来源: 题型:
查看答案和解析>>【题目】码头工人每天往一艘轮船50吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,在(2)的条件下,至少需要增加多少名工人才能完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(1,5)所在的象限是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A. a2+a2=a4 B. (3x)2=6x2 C. (x2)3=x6 D. (x+y)2=x2+y2
-
科目: 来源: 题型:
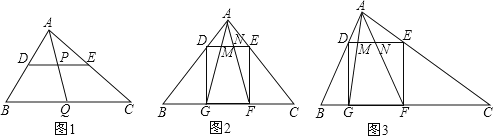
查看答案和解析>>【题目】(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证:
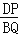 =
=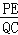 ;
;(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DMEN.
相关试题

