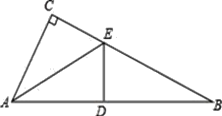
【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B.
(1)如果AC=3cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。
参考答案:
【答案】(1)6cm;(2)ED⊥AB.理由见解析.
【解析】试题分析:(1)先由角平分线的定义及已知条件得出∠CAE=∠EAB=∠B,再根据直角三角形两锐角互余得出∠CAE+∠EAB+∠B=3∠B=90°,那么∠B=30°,根据30°角所对的直角边等于斜边的一半得出AB=2AC=6cm;
(2)先由∠EAB=∠B,根据等角对等边得出EB=EA,又ED平分∠AEB,根据等腰三角形三线合一的性质得到ED⊥AB.
试题解析:(1)∵AE是△ABC的角平分线,
∴∠CAE=∠EAB,
∵∠CAE=∠B,
∴∠CAE=∠EAB=∠B.
∵在△ABC中,∠C=90°,
∴∠CAE+∠EAB+∠B=3∠B=90°,
∴∠B=30°;
又∵∠C=90°,AC=3cm,
∴AB=2AC=6cm .
(2)猜想:ED⊥AB.理由如下:
∵∠EAB=∠B,
∴EB=EA,
∵ED平分∠AEB,
∴ED⊥AB.
故答案为(1)6cm (2)猜想:ED⊥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生动地课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计,下面是整理数据后绘制的两幅不完整的统计图,以下结论不正确的是( )

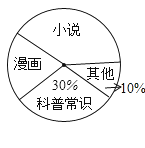
A.由这两个统计图可知喜欢“科学常识”的学生有90人
B.若该年级共有12000名学生,则由这两个统计图可估计喜爱“科学常识”的学生有360人
C.在扇形统计图汇总“漫画”所在扇形的圆心角为72°
D.由这两个统计图不能确定喜欢“小说”的人数 -
科目: 来源: 题型:
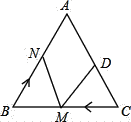
查看答案和解析>>【题目】如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.
①经过2秒后,△BMN和△CDM是否全等?请说明理由.
②当两点的运动时间为多少时,△BMN是一个直角三角形?
(2)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是 厘米/秒.(直接写出答案)
-
科目: 来源: 题型:
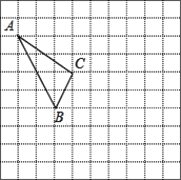
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为A(-4,5),C(-1,3).
(1)请在如图所示的网格内作出x轴、y轴;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标并求出△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a+6和2a﹣15是一个数的平方根,则这个数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A=100°,那么∠A补角为度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中正确的是( )
A. 0既是正数,又是负数 B. O是最小的正数
C. 0是最大的负数 D. 0既不是正数,也不是负数
相关试题

