【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC= ![]() ,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG. 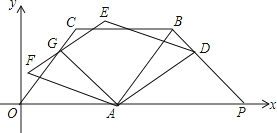
(1)求点B的坐标.
(2)当OG=4时,求AG的长.
(3)求证:GA平分∠OGE.
(4)连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标.
参考答案:
【答案】
(1)
解:如图1,过点B作BH⊥x轴于点H,
∵四边形OABC为菱形,
∴OC∥AB,
∴∠BAH=∠COA.
∵tan∠AOC= ![]() ,
,
∴tan∠BAH= ![]() .
.
又∵在直角△BAH中,AB=5,
∴BH= ![]() AB=4,AH=
AB=4,AH= ![]() AB=3,
AB=3,
∴OH=OA+AH=5+3=8,
∴点B的坐标为(8,4)
(2)
解:如图1,
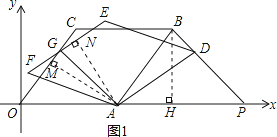
过点A作AM⊥OC于点M,
在直角△AOM中,∵tan∠AOC= ![]() ,OA=5,
,OA=5,
∴AM= ![]() OA=4,OM=
OA=4,OM= ![]() OA=3,
OA=3,
∵OG=4,
∴GM=OG﹣OM=4﹣3=1,
∴AG= ![]() =
= ![]() =
= ![]()
(3)
证明:如图1,

过点A作AN⊥EF于点N,
∵在△AOM与△AFN中, 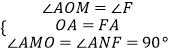 ,
,
∴△AOM≌△AFN(ASA),
∴AM=AN,
∴GA平分∠OGE
(4)
解:如图2,
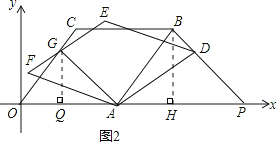
过点G作GQ⊥x轴于点Q,
由旋转可知:∠OAF=∠BAD=α.
∵AB=AD,
∴∠ABP= ![]() ,
,
∵∠AOT=∠F,∠OTA=∠GTF,
∴∠OGA=∠EGA= ![]() ,
,
∴∠OGA=ABP,
又∵∠GOA=∠BAP,
∴△GOA∽△BAP,
∴ ![]() ,
,
∴GQ= ![]() ×4=
×4= ![]() .
.
∵tan∠AOC= ![]() ,
,
∴OQ= ![]() ×
× ![]() =
= ![]() ,
,
∴G( ![]() ,
, ![]() ).
).
【解析】(1)如图1,过点B作BH⊥x轴于点H,构建直角△ABH,所以利用菱形的四条边相等的性质和解该直角三角形得到AH、BH的长度,则易求点B的坐标;(2)如图1,过点A作AM⊥OC于点M,构建直角△OAM和直角△AMG,通过解直角△OAM求得直角边AM的长度,然后结合图形和勾股定理来求AG的长度;(3)如图1,过点A作AM⊥OC于点M,构建全等三角形:△AOM≌△AFN(ASA),利用该全等三角形的对应边相等得到AM=AN,最后结合角平分线的性质证得结论;(4)如图2,过点G作GQ⊥x轴于点Q,构建相似三角形:△GOA∽△BAP,根据该相似三角形的对应边成比例得到求得GQ的长度.结合已知条件tan∠AOC= ![]() ,来求边OQ的长度,即可得到点G的坐标.本题考查了四边形综合题.解题过程中,涉及到了全等三角形的判定与性质,相似三角形的判定与性质,旋转的性质,解直角三角形以及勾股定理等知识点,解答该题的难点在于作出辅助线,构建相关的图形的性质.
,来求边OQ的长度,即可得到点G的坐标.本题考查了四边形综合题.解题过程中,涉及到了全等三角形的判定与性质,相似三角形的判定与性质,旋转的性质,解直角三角形以及勾股定理等知识点,解答该题的难点在于作出辅助线,构建相关的图形的性质.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组.
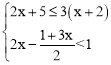 把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.

(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图,反比例函数y=
 与正比例函数y=bx在同一坐标系内的大致图象是( )
与正比例函数y=bx在同一坐标系内的大致图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为cm2 .
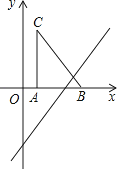
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则
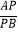 的值= , tan∠APD的值= .
的值= , tan∠APD的值= . 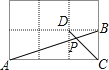
相关试题

