搜索
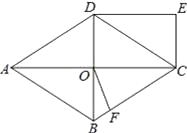
【题目】（6分）如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．
（1）求证：四边形OCED为矩形；
（2）过点O作OF⊥BC，垂足为F，若AC=16，BD=12，则OF= ．
参考答案：
【答案】（1）见解析；（2）4.8
【解析】试题分析：（1）先证明四边形OCED是平行四边形，再由菱形的性质得出对角线互相垂直，得出∠COD=90°，即可得出结论；
（2）由菱形的性质求出OC=
AC=8，OB=BD=6，由勾股定理求出BC，再由△BOC面积的计算方法求出OF即可．
（1）证明：∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠COD=90°，
∴四边形OCED为矩形；
（2）解：∵四边形ABCD是菱形，
∴AC⊥BD，OC=AC=8，OB=BD=6，
由勾股定理得：BC=
=10，
∵△BOC的面积=BCOF=OBOC，
∴OF=
=4.8．
故答案为：4.8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程4x2+1=4x的根的情况是（ ）
A. 没有实数根 B. 只有一个实数根
C. 有两个相等的实数根 D. 有两个不相等的实数根
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲型H1N1流感球形病毒细胞的直径约为0.00000156 m，这个数用科学记数法表示是__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程x2﹣8x﹣1=0配方后可变形为（ ）
A．（x+4）2=17
B．（x+4）2=15
C．（x﹣4）2=17
D．（x﹣4）2=15
-
科目： 来源： 题型：
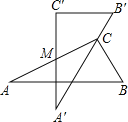
查看答案和解析>>【题目】如图是两块完全一样的含30°角的直角三角板，将它们重叠在一起并绕其较长直角边的中点M转动，使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C．已知AC=5，则这块直角三角板顶点A、A′之间的距离等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD．
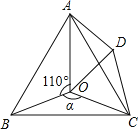
（1）当α=150°时，试判断△AOD的形状，并说明理由；
（2）当△AOD是等腰三角形时，求α的度数．
-
科目： 来源： 题型：
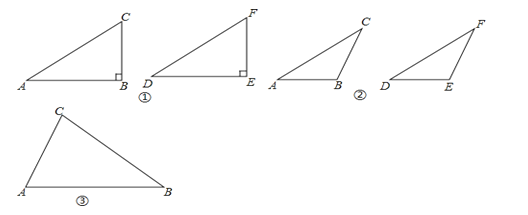
查看答案和解析>>【题目】学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据______，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若______，则△ABC≌△DEF．
相关试题
