【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
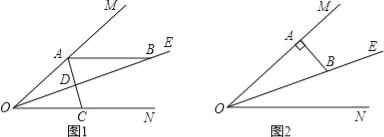
(1)如图1,若AB∥ON,则①∠ABO的度数是 ;
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
参考答案:
【答案】见解析
【解析】试题分析:利用角平分线的性质求出∠ABO的度数是关键,分类讨论的思想.
解:(1)①∵∠MON=40°,OE平分∠MON∴∠AOB=∠BON=20°
∵AB∥ON∴∠ABO=20°
②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°
∵∠BAD=∠BDA,∠ABO=20°∴∠BAD=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°
故答案为:①20 ②120,60
(2)①当点D在线段OB上时,
若∠BAD=∠ABD,则x=20
若∠BAD=∠BDA,则x=35
若∠ADB=∠ABD,则x=50
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=20、35、50、125.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )
A. (-4,3) B. (-3,4) C. (4,-3) D. (3,-4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
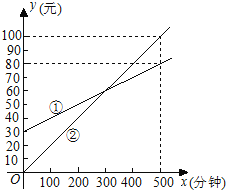
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
-
科目: 来源: 题型:
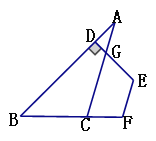
查看答案和解析>>【题目】如图,DE⊥AB,EF∥AC,∠A=32°,
①求∠DEF的度数;
②若∠F比∠ACF大60°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形的边长都为1,将△ABC经过一次平移后得到△A1B1C1,图中标出了点B的对应点B1.
(1)请画出平移后的△A1B1C1;
(2)利用网格画出△ABC 中AC边上的中线BD,高BE;
(3)△A1B1C1的面积为 ;
(4)若△ABP △ABC面积相等,这样的格点P有____个

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:①零是正数;②零是整数;③零是最小的有理数;④零是非负数;⑤零是偶数,正确命题的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正六边形的周长是12,则它的半径是 .
相关试题

