【题目】如图,矩形OABC的顶点A、C分别在![]() 的正半轴上,点B的坐标为(3,4)一次函数
的正半轴上,点B的坐标为(3,4)一次函数![]() 的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是![]() 轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.

参考答案:
【答案】(1)![]() ;
;
(2)M(1, ![]() );
);
(3)当四边形OMDN是菱形时,M(![]() ,
,![]() )N(
)N(![]() ,
,![]() )
)
【解析】分析:(1)首先在一次函数的解析式中令x=0,即可求得D的坐标,则OD的长度即可求得,OD=b,则E的坐标即可利用b表示出来,然后代入一次函数解析式即可得到关于b的方程,求得b的值;(2)首先求得四边形OAED的面积,则△ODM的面积即可求得,设出M的横坐标,根据三角形的面积公式即可求得M的横坐标,进而求得M的坐标;(3)分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论,四边形OMDN是菱形时,M是OD的中垂线与DE的交点,M关于OD的对称点就是N;四边形OMND是菱形,OM=OD,M在直角DE上,设出M的坐标,根据OM=OD即可求得M的坐标,则根据ON和DM的中点重合,即可求得N的坐标.
本题解析:(1)y=![]() x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,
x+b中,令x=0,解得y=b,则D的坐标是(0,b),OD=b,
∵OD=BE,
∴BE=b,则E的坐标是(3,4b),
把E的坐标代入y=![]() x+b得4b=2+b,
x+b得4b=2+b,
解得:b=3;
(2) ![]() ,
,
∵三角形ODM的面积与四边形OAEM的面积之比为1:3,
∴![]() .
.
设M的横坐标是a,则![]() ×3a=1.5,解得:a=1,
×3a=1.5,解得:a=1,
把x=a=1代入y=![]() x+3得y=
x+3得y=![]() ×
×![]() +3=
+3=![]() .
.
则M的坐标是(1, ![]() );
);
(3)当四边形OMDN是菱形时,如图(1),M的纵坐标是![]() ,把y=
,把y=![]() 代入y=
代入y=![]() x+3,得
x+3,得![]() x+3=
x+3=![]() ,解得:x=
,解得:x=![]() ,
,
则M的坐标是(![]() ,
,![]() ),
),
则N的坐标是(![]() ,
,![]() );
);
当四边形OMND是菱形时,如图(2)OM=OD=3,设M的横坐标是m,则纵坐标是![]() m+3,则
m+3,则![]() ,
,
解得:m=![]() 或0(舍去).
或0(舍去).
则M的坐标是(![]() ,
,![]() ).
).
则DM的中点是(![]() ,
,![]() ).
).
则N的坐标是(![]() ,
,![]() ).
).
故N的坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正棱锥有六个顶点,所有侧棱长的和为30cm,则每条侧棱的长是______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是随机事件的是( )
A. 画一个三角形,其内角和是180°
B. 任意画一个四边形,其周长与对角线的和相等
C. 任取一个实数,与其相反数之和为0
D. 外观相同的10件同种产品中有2件是不合格产品,现从中抽取1件即为合格品
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,∠A+∠C=100°,则∠B= ______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度向点C移动(到达点C后停止运动),同时点Q从点A出发,以1cm/s的速度沿AB﹣BC的方向向点C移动(到达点C后停止),若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是图2( )
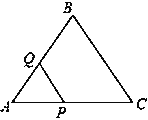
A.
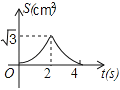 B.
B.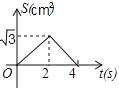 C.
C.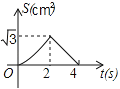 D.
D.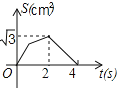
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为
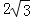 ,则a的值是( )
,则a的值是( )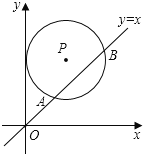
A.2
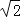 B.2+
B.2+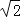 C.2
C.2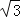 D.2+
D.2+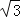
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 处于中间位置的数为这组数据的中位数
B. 中间两个数的平均数为这组数据的中位数
C. 要想了解一批电磁炉的使用寿命,适合采用全面调查的方法
D. 公司员工月收入的众数为3500元.说明该公司中月收入3500元的员工最多
相关试题

