Question

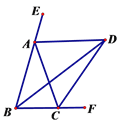
【题目】如图,∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．

以下结论:①AD∥BC； ②∠ACB=2∠ADB； ③∠ADC=90°-∠ABD； ④BD平分∠ADC；⑤∠BDC=∠BAC．其中正确的结论有____________。（填写正确的序号）

Answer 1

【答案】①②③⑤

【解析】分析：根据角平分线定义得出∠ABC=2∠ABD=2∠DBC，∠EAC=2∠EAD，∠ACF=2∠DCF，根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°，根据三角形外角性质得出∠ACF=∠ABC+∠BAC，∠EAC=∠ABC+∠ACB，根据已知结论逐步推理，即可判断各项．

解析∵AD平分∠EAC，

∴∠EAC=2∠EAD，

∵∠EAC=∠ABC+∠ACB，∠ABC=∠ACB，

∴∠EAD=∠ABC，

∴AD∥BC，∴①正确；

∵AD∥BC，

∴∠ADB=∠DBC，

∵BD平分∠ABC，∠ABC=∠ACB，

∴∠ABC=∠ACB=2∠DBC，

∴∠ACB=2∠ADB，∴②正确；

在△ADC中,∠ADC+∠CAD+∠ACD=180，

∵CD平分△ABC的外角∠ACF，

∴∠ACD=∠DCF，

∵AD∥BC，

∴∠ADC=∠DCF，∠ADB=∠DBC，∠CAD=∠ACB

∴∠ACD=∠ADC，∠CAD=∠ACB=∠ABC=2∠ABD，

∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180，

∴∠ADC+∠ABD=90

∴∠ADC=90∠ABD，∴③正确；

∵BD平分∠ABC，

∴∠ABD=∠DBC，

∵∠ADB=∠DBC,∠ADC=9012∠ABC，

∴∠ADB不等于∠CDB，∴④错误；

∵∠ACF=2∠DCF，∠ACF=∠BAC+∠ABC，∠ABC=2∠DBC，∠DCF=∠DBC+∠BDC，

∴∠BAC=2∠BDC，∴⑤正确；

故填①②③⑤.