【题目】如图,在平面直角坐标系中有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 。
。
(1)请直接写出![]() 点坐标。
点坐标。
(2)将![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,
个单位, ![]() 、
、![]() 两点的对应点、正好落在反比例函数
两点的对应点、正好落在反比例函数![]() 在第一象限内图象上。请求出
在第一象限内图象上。请求出![]() ,
, ![]() 的值。
的值。
(3)在(2)的条件下,问是否存![]() 轴上的点
轴上的点![]() 和反比例函数
和反比例函数![]() 图象上的点
图象上的点![]() ,使得以
,使得以![]() 、
、![]() ,
, ![]() ,
, ![]() 为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点
为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点![]() 和点
和点![]() 的坐标;如果不存在,请说明理由。
的坐标;如果不存在,请说明理由。

参考答案:
【答案】(1) ![]() 点坐标为(-4,3);
点坐标为(-4,3);
(2) ![]() 的值为6,
的值为6, ![]() 的值为6;
的值为6;
(3)M的坐标为(6.5,0)N的坐标为(1.5,4),或M的坐标为(7,0)N的坐标为(3,2),或M的坐标为(-7,0)N的坐标为(-3,2)
【解析】试题分析:(1)由在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,可证得△ADC≌△BOA,继而求得C点坐标;
(2)![]() 向右平移了t个单位长度,则点B′的坐标为(t,1)、C′的坐标为(t-3,2),由B′、C′正好落在反比例函数
向右平移了t个单位长度,则点B′的坐标为(t,1)、C′的坐标为(t-3,2),由B′、C′正好落在反比例函数![]() 的图象上,即可得t=2(t-3),继而求得t的值,则可求得k的值 ;
的图象上,即可得t=2(t-3),继而求得t的值,则可求得k的值 ;
(3)进行分类试论出MN的位置,即可得解.
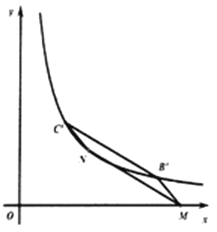
试题解析:(1)如图1,过点C作CD⊥x轴于点D,则∠ADC=∠AOB=90°,
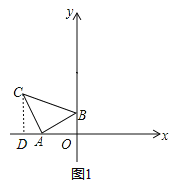
∴∠DAC+∠ACD=90°,
∵Rt△ABC,∠A=90°,
∴∠DAC+∠BAO=90°,
∴∠BAO=∠ACD,
在△ADC和△BOA中,
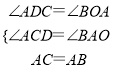 ,
,
∴△ADC≌△BOA(AAS),
∴AD=OB=1,CD=OA=3,
∴OD=OA+AD=4,
∴C点坐标为:(-4,2);
(2)ΔABC向右平移了t个单位长度,则点B′的坐标为(t,1)、C′的坐标为(t-3,2),如图,
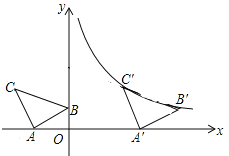
∵B′、C′正好落在反比例函数![]() 图象上,
图象上,
∴t=2(t-3),
解得:t=6,
∴B′(6,1),C′(3,2),
∴k=6;
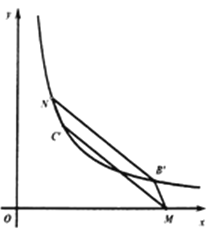
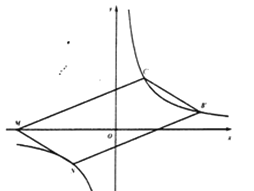
(3)MN平行四边形MCˊNBˊ对角线时,由平行四边形对错爱线互相平分,可知线段BˊCˊ,MN的中点为同一个点,即: ![]() ,yN =4,代入
,yN =4,代入![]() ,得xN=1.5
,得xN=1.5
故N点坐标为(1.5,4)
![]() ,xN=6.5,所以M点的坐标为(6.5,0)
,xN=6.5,所以M点的坐标为(6.5,0)
MCˊ平行四边形MNCˊBˊ对角线时,可得M的坐标为(7,0),N点的坐标为(3,2)
MBˊ平行四边形MCˊBˊN对角线时,可得M的坐标为(-7,0),N点的坐标为(-3,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班的中考英语口语考试成绩如表:
考试成绩/分
30
29
28
27
26
学生数/人
3
15
13
6
3
则该班中考英语口语考试成绩的众数比中位数多___分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初二年学生乘车到距学校40千米的社会实践基地进行社会实践.一部分学生乘旅游车,另一部分学生乘中巴车,他们同时出发,结果乘中巴车的同学晚到8分钟.已知旅游车速度是中巴车速度的1.2倍,求中巴车和旅游车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,张老师说:“
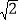 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把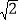 的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(
的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(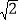 ﹣1)表示它的小数部分.接着,张老师出示了一道练习题:
﹣1)表示它的小数部分.接着,张老师出示了一道练习题:“已知8+
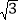 =x+y,其中x是一个整数,且0<y<1,请你求出2x+(
=x+y,其中x是一个整数,且0<y<1,请你求出2x+(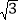 ﹣y)2016的值”.请聪明的你给出正确答案.
﹣y)2016的值”.请聪明的你给出正确答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a2) 4÷a5÷a的结果为 ( )
A. a5 B. a4 C. a3 D. a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】零与任意负数的乘积得_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若圆锥的高是8cm,母线长是10cm,则这个圆锥的侧面积是_____cm2(结果保留π).
相关试题

