【题目】如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.

(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.
参考答案:
【答案】(1)y=x2+2x+1;(2)y=2x+2.
【解析】
试题分析:(1)抛物线与x轴仅有1个交点可知△=0时,即可得到4a2﹣4a=0,解方程即可求得a,即可得到抛物线解析式;(2)先求得A的坐标,已知点C是线段AB的中点,可判定点A与点B的横坐标互为相反数,再确定B点坐标,最后利用待定系数法求直线AB的解析式.
试题解析:
(1)∵抛物线y=ax2+2ax+1与x轴仅有一个公共点A,
∴△=4a2﹣4a=0,解得a1=0(舍去),a2=1,
∴抛物线解析式为y=x2+2x+1;
(2)∵y=(x+1)2,
∴顶点A的坐标为(﹣1,0),
∵点C是线段AB的中点,
即点A与点B关于C点对称,
∴B点的横坐标为1,
当x=1时,y=x2+2x+1=1+2+1=4,则B(1,4),
设直线AB的解析式为y=kx+b,
把A(﹣1,0),B(1,4)代入得,解得,
∴直线AB的解析式为y=2x+2.
-
科目: 来源: 题型:
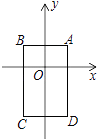
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把弯曲的河道改直,能够缩短航程,这样做的道理是( )
A.两点之间,射线最短
B.两点确定一条直线
C.两点之间,直线最短
D.两点之间,线段最短 -
科目: 来源: 题型:
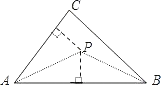
查看答案和解析>>【题目】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB,下列确定P点的方法正确的是( )
A.P是∠A与∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为A
D.AB两边上的高的交点
E.P为A
F.AB两边的垂直平分线的交点 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(3,﹣1)关于y轴的对称点A′的坐标是( )
A. (﹣3,﹣1) B. (3,1) C. (﹣3,1) D. (﹣1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x>y,则x+c_________y+c,5﹣2x_________5﹣2y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形具有而一般平行四边形不具有的性质是( )
A. 对角线相等 B. 对边相等 C. 对角相等 D. 对角线互相平分
相关试题

