【题目】已知二次函数y=(a+2)x2+2ax+a﹣1的图象与x轴有交点,且关于x的分式方程![]() +1=
+1=![]() 的解为整数,则所有满足条件的整数a之和为( )
的解为整数,则所有满足条件的整数a之和为( )
A.﹣4B.﹣6C.﹣8D.3
参考答案:
【答案】A
【解析】
根据二次函数的定义和判别式的意义得到a+2≠0且△=4a2﹣4×(a+2)(a﹣1)≥0,则a≤2且a≠﹣2,再解分式方程得到x=![]() 且x≠﹣1,利用分式方程的解为整数可求出解得a=0,﹣2,1,﹣3,2,﹣4,5,加上a的范围可确定满足条件的a的值,然后计算它们的和.
且x≠﹣1,利用分式方程的解为整数可求出解得a=0,﹣2,1,﹣3,2,﹣4,5,加上a的范围可确定满足条件的a的值,然后计算它们的和.
解:根据题意得a+2≠0且△=4a2﹣4×(a+2)(a﹣1)≥0,
解得a≤2且a≠﹣2,
去分母得ax+x+1=7,
解得x=![]() 且x≠﹣1,
且x≠﹣1,
因为分式方程的解为整数,
所以a+1=±1,±2,±3,±6,且a≠﹣7,
解得a=0,﹣2,1,﹣3,2,﹣4,5,
所以满足条件的a的值为﹣4,﹣3,0,2,1.
所以所有满足条件的整数a之和为﹣4+(﹣3)+0+2+1=﹣4.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由同样大小的黑色圆点按照一定规律所组成的,其中第①个图形中一共有6个黑色圆点第②个图形中一共有15个黑色圆点,第③个图形中一共有28个黑色圆点,…,按此规律排列下去,第⑦个图形中黑色圆点的个数为( )

A.66B.91C.120D.135
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔
 的高度,他从点
的高度,他从点 处的观景塔出来走到点
处的观景塔出来走到点 处.沿着斜坡
处.沿着斜坡 从
从 点走了
点走了 米到达
米到达 点,此时回望观景塔,更显气势宏伟.在
点,此时回望观景塔,更显气势宏伟.在 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为 且
且 ,再往前走到
,再往前走到 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角 ,测得
,测得 之间的水平距离
之间的水平距离 米,则观景塔的高度
米,则观景塔的高度 约为( ) 米. (
约为( ) 米. ( )
)
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y=
 与一次函数y=﹣x+4在第一象限内交于A,B两点,且△AOB的面积为2,则k的值为( )
与一次函数y=﹣x+4在第一象限内交于A,B两点,且△AOB的面积为2,则k的值为( )
A.2B.
 C.
C. D.4
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】1955年,印度数学家卡普耶卡(
 )研究了对四位自然数的一种变换:任给出四位数
)研究了对四位自然数的一种变换:任给出四位数 ,用
,用 的四个数字由大到小重新排列成一个四位数
的四个数字由大到小重新排列成一个四位数 ,再减去它的反序数
,再减去它的反序数 (即将
(即将 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数 ,然后继续对
,然后继续对 重复上述变换,得数
重复上述变换,得数 ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论 是多大的四位数,只要四个数字不全相同,最多进行
是多大的四位数,只要四个数字不全相同,最多进行 次上述变换,就会出现变换前后相同的四位数
次上述变换,就会出现变换前后相同的四位数 ,这个数称为
,这个数称为 变换的核.则四位数9631的
变换的核.则四位数9631的 变换的核为______.
变换的核为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.
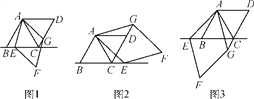
(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:三角形的直角边长/

1
2
3
4
5
6
7
8
9
10
阴影部分的面积/

398
392
382
368
350
302
272
200

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由
 增加到
增加到 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?(4)设等腰直角三角形的直角边长为
 ,图中阴影部分的面积为
,图中阴影部分的面积为 ,写出
,写出 与
与 的关系式.
的关系式.
相关试题

