【题目】先阅读下列的解答过程,然后作答:
形如![]() 的化简,只要我们找到两个数a、b使a+b=m,ab=n,这样(
的化简,只要我们找到两个数a、b使a+b=m,ab=n,这样(![]() )2+(
)2+(![]() )2=m
)2=m![]() ·
·![]() =n,那么便有
=n,那么便有![]() =
=![]() =
=![]() ±
±![]() (a>b) .例如:化简
(a>b) .例如:化简![]() 解:首先把
解:首先把![]() 化为
化为![]() ,这里m=7,n=12;由于4+3=7,4×3=12,即(
,这里m=7,n=12;由于4+3=7,4×3=12,即(![]() )2+(
)2+(![]() )2=7
)2=7![]() ·
·![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =2+
=2+![]() .
.
由上述例题的方法化简:(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析: 先把各题中的无理式变成![]() 的形式,再根据范例分别求出各题中的a、b,即可求解.
的形式,再根据范例分别求出各题中的a、b,即可求解.
试题解析:
(1) ![]() =
= ![]() =
= ![]() -
- ![]() ;
;
(2) ![]() =
= ![]() =
= ![]() =
= ![]() -
- ![]() ;
;
(3) ![]() =
= ![]() =
= ![]()
点睛: 主要考查二次根式根号内含有根号的式子化简.根据二次根式的乘除法法则进行二次根式根号内含有根号的式子化简.二次根式根号内含有根号的式子化简主要利用了完全平方公式,所以一般二次根式根号内含有根号的式子化简是符合完全平方公式的特点的式子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果3m=6,3n=2,那么3m﹣n为
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣5(x+2)2﹣6的对称轴和顶点分别是( )
A. x=2和(2,﹣6) B. x=2和(﹣2,﹣6)
C. x=﹣2和(﹣2,﹣6) D. x=﹣2和(2,﹣6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016重庆市第26题)如图1,二次函数
 的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD//x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+
 BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+ BH的最小值;
BH的最小值;(3)如图2,直线AB上有一点K(3,4),将二次函数
 沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。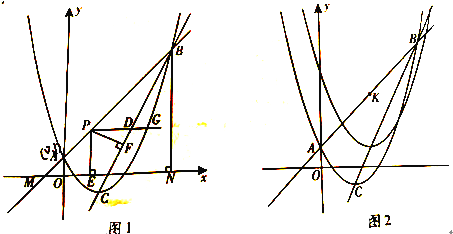
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某学校开展“远是君山,磨砺意志,保护江豚,爱鸟护鸟”为主题的远足活动.已知学校与君山岛相距24千米,远足服务人员骑自行车,学生步行,服务人员骑自行车的平均速度是学生步行平均速度的2.5倍,服务人员与学生同时从学校出发,到达君山岛时,服务人员所花时间比学生少用了3.6小时,求学生步行的平均速度是多少千米/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的分别平行且.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y= -2x的图象经过( )
A.第三、一象限B.第二、四象限C.第二、一象限D.第三、四象限
相关试题

