【题目】如图,直线y=-2x+6与坐标轴分别交于点A,B,正比例函数y=x的图象与直线y=-2x+6交于点C。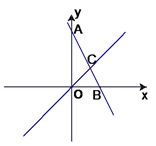
(1)求点A、B的坐标。
(2)求△BOC的面积
(3)已知点P是y轴上的一个动点,求BP+CP的最小值和此时点P的坐标。
参考答案:
【答案】
(1)解:将x=0代入y=-2x+6得y=6
因此A(0,6)
将y=0代入y=-2x+6得x=3
因此B(3,0)
所以A(0,6) ,B(3,0)
(2)解: ![]() 解得
解得 ![]()
所以点C(2,2)
![]()
(3)解:因为点C为(2,2)
作点C关于y轴对称点 ![]() ,
,
连接BC’,由题可得
BP+CP的最小值= BC' = ![]()
由C’(-2,2),B(3,0)可得
直线 BC' 的函数表达式 ![]()
直线 BC' 与y 轴交点即为点P(0, ![]() )
)
【解析】(1)因为点A、B在坐标轴上,所以让横坐标或纵坐标为0,易得A,B坐标。
(2)点C为两个函数的交点,将两个函数连列方程组,所得的结果即为交点C的坐标,易得三角形的面积。
(3)BP+CP的最小值,即为做一点的对称点,并连接对称点与另一点,对称点与另一点所连线段即为最小值,利用勾股定理可得答案;
再利用两点求得直线解析式,与y轴交点即为所求点。
【考点精析】利用一次函数的性质和一次函数的图象和性质对题目进行判断即可得到答案,需要熟知一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是平行四边形,
是平行四边形, ,
, ,
, 是
是 的中点,
的中点, 是
是 延长线上一点.
延长线上一点.
(1)若
 ,求证:
,求证: ;
;(2)在(1)的条件下,若
 的延长线与
的延长线与 交于点
交于点 ,试判定四边形
,试判定四边形 是否为平行四边形?并证明你的结论(请先补全图形,再解答);
是否为平行四边形?并证明你的结论(请先补全图形,再解答);(3)若
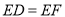 ,
, 与
与 垂直吗?若垂直给出证明,若不垂直说明理由.
垂直吗?若垂直给出证明,若不垂直说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x-y)2-(y-x)2-(x+y)(y-x),其中x=3,y=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,边AB、AC的垂直平分线分别交边BC于点D、E,若∠DAE=40°,则∠BAC的度数为________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,且△ABC 的周长为 12,若 AB=3,EF=4,则 AC=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为时,能够在某一时刻使△BPD与△CQP全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
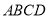 中,
中,  ,
, 平分
平分 ,点
,点 是
是 延长线上一点,且
延长线上一点,且 .
.
(1)证明:
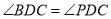 ;
;(2)若
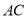 与
与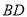 相交于点
相交于点 ,
, ,
, ,求
,求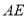 的长.
的长.
相关试题

