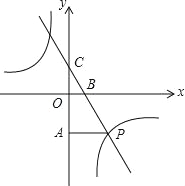
【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
参考答案:
【答案】(1)反比例函数的表达式为y=﹣![]() ;
;
(2)点Q的坐标为(﹣![]() ,9)或(
,9)或(![]() ,﹣3).
,﹣3).
【解析】
试题分析:(1)由一次函数表达式可得出点C的坐标,结合A点坐标以及三角形的面积公式可得出AP的长度,从而得出点P的坐标,由点P的坐标结合待定系数法即可求出一次函数及反比例函数的表达式;
(2)设点Q的坐标为(m,﹣![]() m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
试题解析:(1)令一次函数y=kx+3中的x=0,则y=3,
即点C的坐标为(0,3),
∴AC=3﹣(﹣6)=9.
∵S△CAP=![]() ACAP=18,
ACAP=18,
∴AP=4,
∵点A的坐标为(0,﹣6),
∴点P的坐标为(4,﹣6).
∵点P在一次函数y=kx+3的图象上,
∴﹣6=4k+3,解得:k=﹣![]() ;
;
∵点P在反比例函数y=![]() 的图象上,
的图象上,
∴﹣6=![]() ,解得:n=﹣24.
,解得:n=﹣24.
∴一次函数的表达式为y=﹣![]() x+3,反比例函数的表达式为y=﹣
x+3,反比例函数的表达式为y=﹣![]() .
.
(2)令一次函数y=﹣![]() x+3中的y=0,则0=﹣
x+3中的y=0,则0=﹣![]() x+3,解得:x=
x+3,解得:x=![]() ,
,
即点B的坐标为(![]() ,0).设点Q的坐标为(m,﹣
,0).设点Q的坐标为(m,﹣![]() m+3).
m+3).
∵△OCQ的面积是△BCO面积的2倍,
∴|m|=2×![]() ,解得:m=±
,解得:m=±![]() ,
,
∴点Q的坐标为(﹣![]() ,9)或(
,9)或(![]() ,﹣3).
,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有一个呈等腰直角三角形的积木盒,现在积木盒中只剩下如图1所示的九个空格,图2是可供选择的A、B、C、D四块积木.
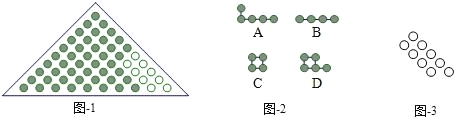
(1)小明选择把积木A和B放入图3,要求积木A和B的九个小圆恰好能分别与图3中的九个小圆重合,请在图3中画出他放入方式的示意图(温馨提醒:积木A和B的连接小圆的小线段还是要画上哦!);
(2)现从A、B、C、D四块积木中任选两块,求恰好能全部不重叠放入的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一根铁丝正好可以围成一个长是2a+3b,宽是a+b的长方形框,把它剪去一部分后,剩余的铁丝可围成一个长是a,宽是b的长方形框(均不计接缝),则剪去部分铁丝总长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明做题一向比较粗心,下面四个题他只做对了一道,他做对的那道题是( )
A.x4+x4=x8B.a2a4=a8
C.﹣a7a5=﹣a12D.(2x2y3)2=﹣2x5y6
-
科目: 来源: 题型:
查看答案和解析>>【题目】补充完整:(-a-b+c)(a-b+c)=-[a+(_______)][a-(________)].
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.任何实数都有平方根
B.两个整数相除,永远都除不尽,结果一定是无理数
C.有理数与数轴上的点一一对应
D.任意一个无理数的绝对值都是正数
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方体的长为(a+2)cm,宽为(a+1)cm,高为(a﹣1)cm,则它的表面积为( )cm2.
A.3a2+4a﹣1B.6a2+8a﹣2C.6a+4D.3a+2
相关试题

