【题目】如图1,抛物线![]() 经过平行四边形
经过平行四边形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() ,抛物线与
,抛物线与![]() 轴的另一交点为
轴的另一交点为![]() .经过点
.经过点![]() 的直线
的直线![]() 将平行四边形
将平行四边形![]() 分割为面积相等的两部分,与抛物线交于另一点
分割为面积相等的两部分,与抛物线交于另一点![]() .点
.点![]() 为直线
为直线![]() 上方抛物线上一动点,设点
上方抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当![]() 何值时,
何值时,![]() 的面积最大?并求最大值的立方根;
的面积最大?并求最大值的立方根;
(3)是否存在点![]() 使
使![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

参考答案:
【答案】(1)抛物线解析式为y=﹣x2+2x+3;(2)当t=![]() 时,△PEF的面积最大,其最大值为
时,△PEF的面积最大,其最大值为![]() ×
×![]() ,
,
最大值的立方根为![]() =
=![]() ;(3)存在满足条件的点P,t的值为1或
;(3)存在满足条件的点P,t的值为1或![]()
【解析】
试题分析:(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)由A、C坐标可求得平行四边形的中心的坐标,由抛物线的对称性可求得E点坐标,从而可求得直线EF的解析式,作PH⊥x轴,交直线l于点M,作FN⊥PH,则可用t表示出PM的长,从而可表示出△PEF的面积,再利用二次函数的性质可求得其最大值,再求其最大值的立方根即可;
(3)由题意可知有∠PAE=90°或∠APE=90°两种情况,当∠PAE=90°时,作PG⊥y轴,利用等腰直角三角形的性质可得到关于t的方程,可求得t的值;当∠APE=90°时,作PK⊥x轴,AQ⊥PK,则可证得△PKE∽△AQP,利用相似三角形的性质可得到关于t的方程,可求得t的值.
试题解析: (1)由题意可得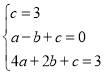 ,解得
,解得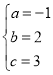 ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵A(0,3),D(2,3),
∴BC=AD=2,
∵B(﹣1,0),
∴C(1,0),
∴线段AC的中点为(![]() ,
,![]() ),
),
∵直线l将平行四边形ABCD分割为面积相等两部分,
∴直线l过平行四边形的对称中心,
∵A、D关于对称轴对称,
∴抛物线对称轴为x=1,
∴E(3,0),
设直线l的解析式为y=kx+m,把E点和对称中心坐标代入可得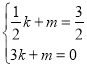 ,解得
,解得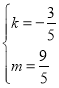 ,
,
∴直线l的解析式为y=﹣![]() x+
x+![]() ,
,
联立直线l和抛物线解析式可得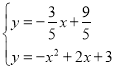 ,解得
,解得![]() 或
或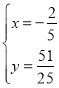 ,
,
∴F(﹣![]() ,
,![]() ),
),
如图1,作PH⊥x轴,交l于点M,作FN⊥PH,
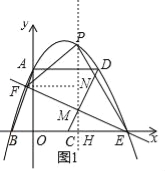
∵P点横坐标为t,
∴P(t,﹣t2+2t+3),M(t,﹣![]() t+
t+![]() ),
),
∴PM=﹣t2+2t+3﹣(﹣![]() t+
t+![]() )=﹣t2+
)=﹣t2+![]() t+
t+![]() ,
,
∴S△PEF=S△PFM+S△PEM=![]() PMFN+
PMFN+![]() PMEH=
PMEH=![]() PM(FN+EH)=
PM(FN+EH)=![]() (﹣t2+
(﹣t2+![]() t+
t+![]() )(3+
)(3+![]() )=﹣
)=﹣![]() (t﹣
(t﹣![]() )+
)+![]() ×
×![]() ,
,
∴当t=![]() 时,△PEF的面积最大,其最大值为
时,△PEF的面积最大,其最大值为![]() ×
×![]() ,
,
∴最大值的立方根为![]() =
=![]() ;
;
(3)由图可知∠PEA≠90°,
∴只能有∠PAE=90°或∠APE=90°,
①当∠PAE=90°时,如图2,作PG⊥y轴,
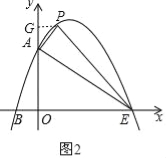
∵OA=OE,
∴∠OAE=∠OEA=45°,
∴∠PAG=∠APG=45°,
∴PG=AG,
∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),
②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,
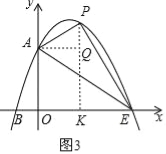
则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,
∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,
∴∠PAQ=∠KPE,且∠PKE=∠PQA,
∴△PKE∽△AQP,
∴![]() ,即
,即![]() ,即t2﹣t﹣1=0,解得t=
,即t2﹣t﹣1=0,解得t=![]() 或t=
或t=![]() <﹣
<﹣![]() (舍去),
(舍去),
综上可知存在满足条件的点P,t的值为1或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比2的相反数小的是( )
A.5
B.﹣3
C.0
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:4a2b÷2ab=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
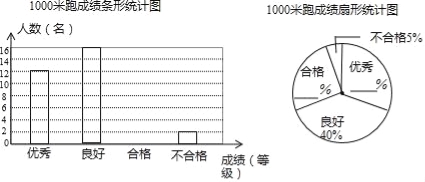
(1)根据给出的信息,补全两幅统计图;
(2)该校九年级有600名男生,请估计成绩未达到良好有多少名?
(3)某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛,预赛分为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:
 ≈1.73).
≈1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据龙岗城市发展建设需要,政府计划增加固定资产投资152亿元,确保项目更新得到落实,152亿元用科学记数法表示为元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为6的等边
 中,点
中,点 、
、 分别在
分别在 、
、 边上,
边上,  ,
,  .
. 
(l)如图1,将
 沿射线
沿射线 方向平移,得到
方向平移,得到 ,边
,边 与
与 的交点为
的交点为 ,边
,边 与
与 的角平分线交于点
的角平分线交于点 .当
.当 多大时,四边形
多大时,四边形 为菱形?并说明理由.
为菱形?并说明理由. (2)如图2,将
 绕点
绕点 旋转
旋转 (
( ),得到
),得到 ,连接
,连接 、
、 ,边
,边 的中点为
的中点为 .
. ①在旋转过程中,
 和
和 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.②连接
 ,当
,当 最大时,求
最大时,求 的值.(结果保留根号)
的值.(结果保留根号)
相关试题

