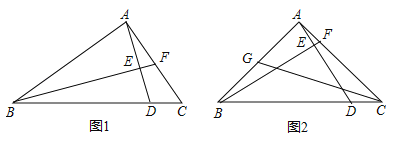
【题目】如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．

（1）如图1，若BD=BA，求证：△ABE≌△DBE；

（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AFAC．

参考答案：

【答案】（1）证明见解析；（2）①证明见解析；②证明见解析．

【解析】

试题分析：（1）根据全等三角形的判定定理即可得到结论；

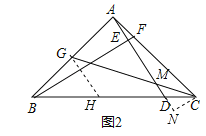
（2）①过G作GH∥AD交BC于H，由AG=BG，得到BH=DH，根据已知条件设DC=1，BD=4，得到BH=DH=2，根据平行线分线段成比例定理得到，求得GM=2MC；

②过C作CN⊥AD交AD的延长线于N，则CN∥AG，根据相似三角形的性质得到，由①知GM=2MC，得到2NC=AG，根据相似三角形的性质得到，等量代换得到，于是得到结论．

试题解析：（1）在Rt△ABE和Rt△DBE中，∵BA=BD，BE=BE，∴△ABE≌△DBE；

（2）①过G作GH∥AD交BC于H，∵AG=BG，∴BH=DH，∵BD=4DC，设DC=1，BD=4，∴BH=DH=2，∵GH∥AD，∴，∴GM=2MC；

②过C作CN⊥AC交AD的延长线于N，则CN∥AG，∴△AGM∽△NCM，∴，由①知GM=2MC，∴2NC=AG，∵∠BAC=∠AEB=90°，∴∠ABF=∠CAN=90°﹣∠BAE，∴△ACN∽△BAF，∴，∵AB=AG，∴，∴2CNAG=AFAC，∴AG2=AFAC．

关闭