【题目】如图所示,抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,
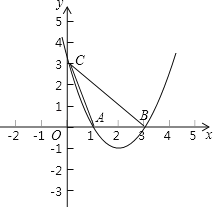
(1)求cos∠CAO的值;
(2)求直线AC的函数关系式;
(3)如果有动点P是y轴上,且△OPA与△OAC相似,求P点坐标.
参考答案:
【答案】(1)cos∠CAO=![]() ;(2)直线AC的解析式为:y=﹣3x+3;(3)点P的坐标为:(0,﹣3),(0,
;(2)直线AC的解析式为:y=﹣3x+3;(3)点P的坐标为:(0,﹣3),(0,![]() ),(0,﹣
),(0,﹣![]() ).
).
【解析】
试题分析:(1)根据抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,可以求得A、B、C三点的坐标,从而可以求得OA、OC、AC的长,进而可以得到cos∠CAO的值;
(2)根据点A、C两点的坐标,可以求得直线AC的函数关系式;
(3)根据第三问的条件,可知符合要求的三角形OPA存在三种情况,然后分别画出相应的图形,即可求得点P的坐标.
解:(1)∵抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,
∴x2﹣4x+3=0,得x=1或x=3,x=0时,y=3,
∴点A的坐标为(1,0),点B的坐标为(3,0),点C的坐标为(0,3),
∴OA=1,OC=3,
∴![]() ,
,
∴cos∠CAO=![]() ;
;
(2)设直线AC的解析式为:y=kx+b,
∵点A的坐标为(1,0),点C的坐标为(0,3),
∴![]()
解得k=﹣3,b=3.
即直线AC的解析式为:y=﹣3x+3;
(3)如果有动点P是y轴上,且△OPA与△OAC相似,
则有如下三种情况,
第一种情况如下图1所示,
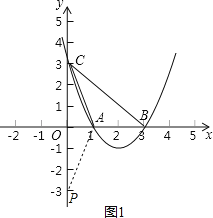
当∠OPA=∠OCA,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),
∴OP=OC=3,
∴点P的坐标为(0,﹣3);
第二种情况如下图2所示,点P位于y轴正半轴,
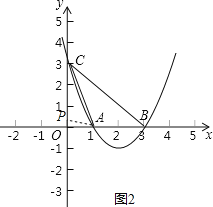
当∠OPA=∠OAC,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),点A的坐标为(1,0),
∴OA=1,OC=3,
∴![]() ,
,
即点P的坐标为(0,![]() );
);
第三种情况如下图3所示,点P位于y轴负半轴,
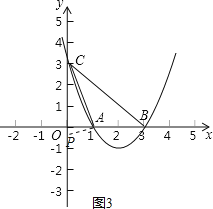
当∠OPA=∠OAC,∠AOC=∠AOP时,△OPA∽△OAC,
∴![]() ,
,
∵点C的坐标为(0,3),点A的坐标为(1,0),
∴OA=1,OC=3,
∴![]() ,
,
即点P的坐标为(0,﹣![]() ).
).
由上可得,点P的坐标为:(0,﹣3),(0,![]() ),(0,﹣
),(0,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某频数分布直方图中,共有A,B,C,D,E五个小组,频数分别为10,15,25,35,10,则直方图中,长方形高的比为( )
A. 2∶3∶5∶7∶2 B. 1∶3∶4∶5∶1 C. 2∶3∶5∶6∶2 D. 2∶4∶5∶4∶2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
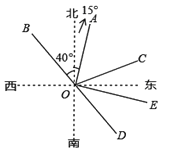
(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2016的值为( )
A.﹣1007
B.﹣1008
C.﹣1009
D.﹣1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AD为正△ABC的高.
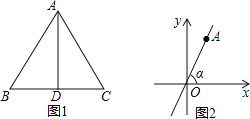
(1)利用此图形填表:
30°
60°
sin
cos
tan
(2)利用(1)题中结论,计算:(
 )﹣1﹣3tan60°+
)﹣1﹣3tan60°+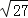
(3)利用(1)题中结论解答:如图2,直线l:y=
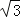 x与x轴所夹的锐角为α,直线l上点A的横坐标为1,求∠α.
x与x轴所夹的锐角为α,直线l上点A的横坐标为1,求∠α. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
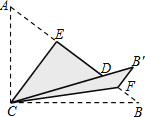
A.
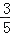 B.
B.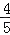 C.
C. D.
D.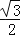
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型超市国庆期间举行促销活动. 假定一次购物不超过100元的不给优惠;超过100元而不超过300元时,按该次购物金额9折优惠;超过300元的其中300元仍按9折优惠,超过300元部分按8折优惠. 小美两次购物分别用了94.5元和282.8元,现小丽决定一次购买小美分两次购买的同样的物品,应付款多少元?
相关试题

