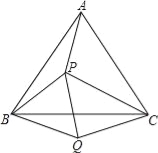
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是( )
A.△BPQ是等边三角形
B.△PCQ是直角三角形
C.∠APB=150°
D.∠APC=135°
参考答案:
【答案】D
【解析】
试题分析:根据等边三角形性质得出∠ABC=60°,根据全等得出∠BPA=∠BQC,BP=BQ=4,QC=PA=3,∠ABP=∠QBC,求出∠PBQ=60°,即可判断A,根据勾股定理的逆定理即可判断B;求出∠BQP=60°,∠PQC=90°,即可判断C,求出∠APC+∠QPC=150°和PQ≠QC即可判断D.
∵△ABC是等边三角形, ∴∠ABC=60°, ∵△BQC≌△BPA,
∴∠BPA=∠BQC,BP=BQ=4,QC=PA=3,∠ABP=∠QBC,
∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,
∴△BPQ是等边三角形, ∴PQ=BP=4, ∵PQ2+QC2=42+32=25,PC2=52=25, ∴PQ2+QC2=PC2,
∴∠PQC=90°,即△PQC是直角三角形, ∵△BPQ是等边三角形, ∴∠BOQ=∠BQP=60°,
∴∠BPA=∠BQC=60°+90°=150°, ∴∠APC=360°﹣150°﹣60°﹣∠QPC=150°﹣∠QPC,
∵∠PQC=90°,PQ≠QC, ∴∠QPC≠45°,即∠APC≠135°, ∴选项A、B、C正确,选项D错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足
 +
+ =
= ,则
,则 C=90
C=90 ;
;③△ABC中,若
 A:
A:  B:
B:  C=1:5:6,则△ABC是直角三角形;
C=1:5:6,则△ABC是直角三角形;④△ABC中,若a:b:c=1:2:
 ,则这个三角形是直角三角形。
,则这个三角形是直角三角形。其中,错误的说法的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动叫做,这个定点叫做,转动的角叫做角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的平方根是( )
A.8
B.4
C.±4
D.±2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,下列说法正确的是( )
A.两直线的位置关系是平行、垂直和相交
B.不平行的两条直线一定互相垂直
C.不垂直的两条直线一定互相平行
D.不相交的两条直线一定互相平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=
 CM+
CM+ BN.
BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为|AB|.
(1)当A,B两点中有一点在原点时,假设点A在原点,如图①所示,|AB|=|OB|=|b|=|a-b|.


① ②


③ ④
(2)当A,B两点都不在原点时
①如图②所示,点A,B都在原点的右边时,|AB|=|OB|-|OA|=b-a=|a-b|;
②如图③所示,点A,B都在原点的左边时,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|.
③如图④所示,点A,B在原点的两侧时,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|.
解答下列问题:
(1)数轴上表示4与2015的两点之间的距离为________,数轴上表示-
 与-
与-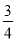 的两点之间的距离为________,数轴上表示1.28与-8.62的两点之间的距离为__________.
的两点之间的距离为________,数轴上表示1.28与-8.62的两点之间的距离为__________.(2)有理数-6和x在数轴上的对应点分别为点A、B,如果|AB|=10,那么x为_________.
相关试题

