搜索
【题目】已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC=6cm，AC=8cm，∠ABD=45°．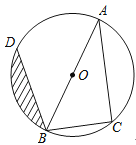
（1）求BD的长
（2）求图中阴影部分的面积
参考答案：
【答案】
（1）
解：∵AB为⊙O的直径，∴∠ACB=90°，∵BC=6cm，AC=8cm，∴AB=10cm．∴OB=5cm．连OD，∵OD=OB，∴∠ODB=∠ABD=45°．
∴∠BOD=90°．∴BD=
=5
cm
（2）
解：S阴影=S扇形﹣S△OBD=
π52﹣
×5×5=
cm2
【解析】（1）由AB为⊙O的直径，得到∠ACB=90°，由勾股定理求得AB，OB=5cm．连OD，得到等腰直角三角形，根据勾股定理即可得到结论；
（2）根据S阴影=S扇形﹣S△OBD即可得到结论．
（1）由AB为⊙O的直径，得到∠ACB=90°，由勾股定理求得AB，OB=5cm．连OD，得到等腰直角三角形，根据勾股定理即可得到结论；
（2）根据S阴影=S扇形﹣S△OBD即可得到结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y=
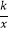（x＞0）的图象经过矩形OABC对角线的交点M，分别与AB、BC相交于点D、E．，则下列结论正确的是（将正确的结论填在横线上）．
①s△OEB=s△ODB ， ②BD=4AD，③连接MD，S△ODM=2S△OCE ， ④连接ED，则△BED∽△BCA．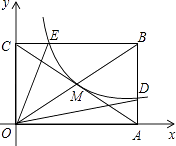
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒，
（1）写出数轴上点B所表示的数 ；
（2）点P所表示的数 ；（用含t的代数式表示）；
（3）M是AP的中点，N为PB的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，说明理由；若不变，请你画出图形，并求出线段MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过点A（﹣1，0），B（0，﹣
），C（2，0），其对称轴与x轴交于点D
（1）求二次函数的表达式及其顶点坐标；
（2）若P为y轴上的一个动点，连接PD，则
PB+PD的最小值为；
（3）M（x，t）为抛物线对称轴上一动点
①若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，则这样的点N共有 个；
②连接MA，MB，若∠AMB不小于60°，求t的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠BAC=90°，AB=AC，点D为射线BC上一点，连接AD，以AD为直角边在AD的右侧作Rt△ADE，且AD=AE.
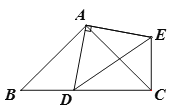
（1）填空：当点D在线段BC上时（与点B不重合），则线段CE、BD的数量关系应为________________,线段CE所在的直线与射线BC的位置关系为____________；
（2）如下图，当点D在线段BC的延长线上时，（1）中的结论是否仍然成立，请证明；
（3）如下图，点D在BC的延长线上，如果AC＝
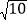cm，△CDE的面积为4cm2时，求线段DE的长度.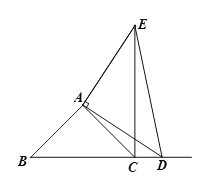
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的对角线相交于点O，点M，N分别是边BC，CD上的动点（不与点B，C，D重合），AM，AN分别交BD于点E，F，且∠MAN始终保持45°不变．
（1）求证：
= 
；
（2）求证：AF⊥FM；
（3）请探索：在∠MAN的旋转过程中，当∠BAM等于多少度时，∠FMN=∠BAM？写出你的探索结论，并加以证明． -
科目： 来源： 题型：
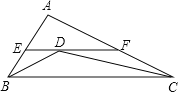
查看答案和解析>>【题目】如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关系（ ）
A.
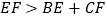B. 
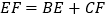C.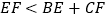 
D. 不能确定
相关试题
