【题目】如图,已知:在矩形ABCD中,O为AC的中点,直线l经过点B,且直线l绕着点B旋转,AM⊥l于点M,CN⊥l于点N,连接OM,ON
(1)当直线l经过点D时,如图1,则OM、ON的数量关系为 ;
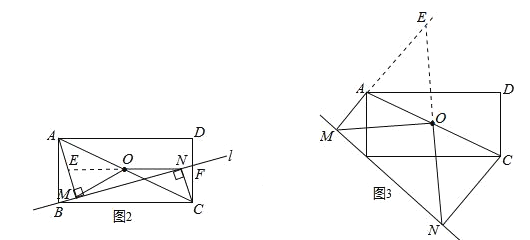
(2)当直线l与线段CD交于点F时,如图2(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由;
(3)当直线l与线段DC的延长线交于点P时,请在图3中作出符合条件的图形,并判断(1)中的结论是否仍然成立?不必说明理由.

参考答案:
【答案】(1)OM=ON;(2)结论仍然成立.(3)结论仍然成立.
【解析】
试题分析:(1)OM=ON;易证△AOM≌△CON,所以OM=ON;
(2)结论仍然成立.如答图2,作辅助线,证明△AEO≌△CNO,得点O为Rt△MEN斜边上的中点,所以OM=ON结论成立;
(3)结论仍然成立.与(2)同理.
试题解析:(1)OM=ON;如题图1,
∵O为AC的中点,
∴OA=OB,
∵AM⊥l于点M,CN⊥l于点N,
∴∠AMO=∠CNO=90°,
在△AMO和△CNO中,
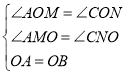 ,
,
∴△AMO≌△CNO(AAS)
∴OM=ON;
(2)(1)中的结论仍然成立.理由如下:
如答图2,延长NO,交AM于点E,
∵AM⊥l于点M,CN⊥l于点N,
∴AM∥CN,
∴∠OAE=∠OCN.
∵矩形ABCD,点O为对角线AC中点,
∴OA=OC.
在△AEO和△CNO中,
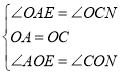
∴△AEO≌△CNO(ASA)
∴OE=ON,
∵Rt△MEN,点O为EN的中点
∴OM=ON(直角三角形斜边上的中线等于斜边的一半).
(3)(1)中的结论仍然成立.理由如下:
如答图3,延长NO,交MA的延长线于点E.
与(2)同理,可以证明OM=ON.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2-4x-4化为y=a(x-h)2+k的形式,正确的是( )
A. y=(x-2)2 B. y=(x+2)2-8
C. y=(x+2)2 D. y=(x-2)2-8
-
科目: 来源: 题型:
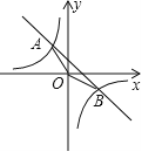
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象与反比例函数
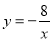 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“早穿皮袄午穿纱”这句民谣形象地描绘了我们新疆奇妙的气温变化现象.乌鲁木齐市五月的某一天,最低气温是t ℃,温差是15 ℃,则当天的最高气温是________℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(x,3)与点B(2,y)关于x轴对称,则( )
A. x=2,y=3 B. x=2,y=-3 C. x=-2,y=3 D. x=-2,y=-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 有限小数不是有理数 B. 无限小数是无理数
C. 数轴上的点与有理数一一对应 D. 数轴上的点与实数一一对应
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形具有而矩形不具有的性质是( )
A. 对角相等B. 对角线互相平分C. 四边相等D. 四角相等
相关试题

