【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
A.AE=6cm
B.sin∠EBC= ![]()
C.当0<t≤10时,y= ![]() t2
t2
D.当t=12s时,△PBQ是等腰三角形
参考答案:
【答案】D
【解析】解:(1)结论A正确.理由如下:
分析函数图象可知,BC=10cm,ED=4cm,故AE=AD﹣ED=BC﹣ED=10﹣4=6cm;(2)结论B正确.理由如下:
如答图1所示,连接EC,过点E作EF⊥BC于点F,
由函数图象可知,BC=BE=10cm,S△BEC=40= ![]() BCEF=
BCEF= ![]() ×10×EF,∴EF=8,
×10×EF,∴EF=8,
∴sin∠EBC= ![]() =
= ![]() =
= ![]() ;(3)结论C正确.理由如下:
;(3)结论C正确.理由如下:
如答图2所示,过点P作PG⊥BQ于点G,
∵BQ=BP=t,
∴y=S△BPQ= ![]() BQPG=
BQPG= ![]() BQBPsin∠EBC=
BQBPsin∠EBC= ![]() tt
tt ![]() =
= ![]() t2 . (4)结论D错误.理由如下:
t2 . (4)结论D错误.理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,设为N,如答图3所示,连接NB,NC.
此时AN=8,ND=2,由勾股定理求得:NB= ![]() ,NC=
,NC= ![]() ,
,
∵BC=10,
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形.
由图2可知,在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:(1)在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数;(2)在ED段,y=40是定值,持续时间4s,则ED=4;(3)在DC段,y持续减小直至为0,y是t的一次函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6cm,BC=4cm.动点E从点B出发,沿着线路BC→CD→DA运动,在BC段的平均速度是1cm/s,在CD段的平均速度是2cm/s,在DA段的平均速度是4cm/s,到点A停止.设△ABE的面积为y(cm2),则y与点E的运动时间t(s)的函数关系图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )
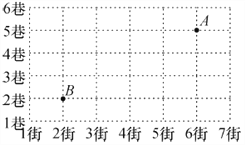
A. (2,2)→(2,5)→(5,6) B. (2,2)→(2,5)→(6,5)
C. (2,2)→(6,2)→(6,5) D. (2,2)→(2,3)→(6,3)→(6,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.

(1)请你写出其他各点C,D,E,F所表示的意义;
(2)若一只兔子从A到达B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B,帮可爱的小白兔选一条路,使它吃到的食物最多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,将一块等腰直角三角板的锐角顶点与A重合,并将三角板绕A点旋转,如图1,使它的斜边与BD交于点H,一条直角边与CD交于点G.
(1)请适当添加辅助线,通过三角形相似,求出
 的值;
的值;(2)连接GH,判断GH与AF的位置关系,并证明;
(3)如图2,将三角板旋转至点F恰好在DC的延长线上时,若AD=
 ,AF=
,AF= .求DG的长.
.求DG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M(a,b)是平面直角坐标系xOy中的点,其中a是从l,2,3,4三个数中任取的一个数,b是从l,2,3,4,5五个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件Qn(2≤n≤9,n为整数),则当Qn的概率最大时,n的所有可能的值为( )
A.5
B.4或5
C.5或6
D.6或7
相关试题

