【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
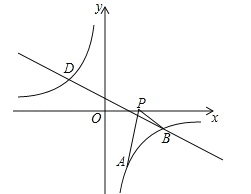
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
参考答案:
【答案】(1)y=x﹣4;(2)P(4,0).
【解析】
试题分析:(1)先把A(1,a)代入反比例函数解析式求出a得到A点坐标,再解方程组 ,得B点坐标,然后利用待定系数法求AB的解析式;
,得B点坐标,然后利用待定系数法求AB的解析式;
(2)直线AB交x轴于点Q,如图,利用x轴上点的坐标特征得到Q点坐标,则PA﹣PB≤AB(当P、A、B共线时取等号),于是可判断当P点运动到Q点时,线段PA与线段PB之差达到最大,从而得到P点坐标.
试题解析:(1)把A(1,a)代入![]() 得a=﹣3,则A(1,﹣3),解方程组:
得a=﹣3,则A(1,﹣3),解方程组: ,得:
,得:![]() 或
或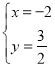 ,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得:
,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得:![]() ,解得:
,解得:![]() ,所以直线AB的解析式为y=x﹣4;
,所以直线AB的解析式为y=x﹣4;
(2)直线AB交x轴于点Q,如图,当y=0时,x﹣4=0,解得x=4,则Q(4,0),因为PA﹣PB≤AB(当P、A、B共线时取等号),所以当P点运动到Q点时,线段PA与线段PB之差达到最大,此时P点坐标为(4,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+bx+c的图象上有两点(3,4)和(﹣5,4),则此拋物线的对称轴是直线( )
A. x=﹣1 B. x=1 C. x=2 D. x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
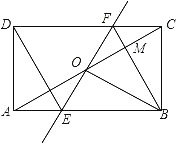
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2÷x2=1
B.(﹣a2b)3=a6b3
C.(﹣3x)0=﹣1
D.(x+3)2=x2+9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )

A. (2015,0) B. (2015,1) C.(2015,2) D.(2016,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三根木棒首尾相接,能做成三角形框架的是( )
A. 1cm、2cm、3cm B. 2cm、3cm、4cm
C. 4cm、9cm、4cm D. 2cm、1cm、4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对数互为相反数的是( )
A. +(﹣3)与﹣3 B. ﹣(﹣3)与+(﹣3)
C. +(+3)与+3 D. ﹣(+3)与+(﹣3)
相关试题

