【题目】如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,求证:
(1)△AEB∽△OFC;
(2)AD=2FO.

参考答案:
【答案】(1)证明见解析.(2)证明见解析.
【解析】试题分析:(1)连接OB,利用三线合一和圆周角定理得出∠BAE=∠COF,根据条件可得∠OFC=∠AEB=90°,然后即可得出结论;(2)利用(1)中△AEB∽△OFC得出![]() ,根据条件证明△ADE∽△BCE得出
,根据条件证明△ADE∽△BCE得出![]() ,进而得出
,进而得出![]() ,然后利用垂经定理即可证出结论.
,然后利用垂经定理即可证出结论.
试题解析:(1)如图,连接OB,

则∠BAE=![]() ∠BOC,
∠BOC,
∵OF⊥BC,
∴∠COF=![]() ∠BOC,
∠BOC,
∴∠BAE=∠COF,
又∵AC⊥BD,OF⊥BC,
∴∠OFC=∠AEB=90°
∴△AEB∽△OFC,
(2)∵△AEB∽△OFC,
∴![]()
即![]()
由圆周角定理,∠D=∠BCE,∠DAE=∠CBE,
∴△ADE∽△BCE。
∴![]()
∴![]()
∵OF⊥BC
∴BC=2CF
∴AD =2FO
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果 (a 1) x a 1 的解集是 x 1 ,那么 a 的取值范围是( )
A.a 0B.a 1C.a 1D.a 是任意有理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=
 ,
,∠ABE=
 .( )
.( )∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】任意一个正整数都可以进行这样的分解:
 (
( 是正整数,且
是正整数,且 ),正整数的所有这种分解中,如果
),正整数的所有这种分解中,如果 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称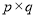 是正整数的最佳分解.并规定:
是正整数的最佳分解.并规定:  .例如24可以分解成1×24,2×12,3×8或4×6,因为
.例如24可以分解成1×24,2×12,3×8或4×6,因为 ,所以4×6是24的最佳分解,所以
,所以4×6是24的最佳分解,所以 .
.(1)求
 的值;
的值;(2)如果一个两位正整数,
 (
( 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为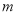 ,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为
,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为 ,若
,若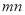 为4752,那么我们称这个数为“最美数”,求所有“最美数”;
为4752,那么我们称这个数为“最美数”,求所有“最美数”;(3)在(2)所得“最美数”中,求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若 7x3ay4b与2x3y3ba是同类项,则ab=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举办了一次以“阳光少年,我们是好伙伴”为主题的演讲比赛,有9名同学参加了决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )
A.平均数B.众数C.中位数D.方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某礼品制造工厂接受一批玩具熊的订货任务,按计划天数生产,如果每天生产20个玩具熊,则比订货任务少100个;如果每天生产23个玩具熊,则可以超过订货任务20个.请求出该厂计划几天完成任务?
相关试题

