【题目】已知等腰△ABC的顶角∠A=36°(如图). 
(1)请用尺规作图法作底角∠ABC的平分线BD,交AC于点D(保留作图痕迹,不要求写作法);
(2)证明:△ABC∽△BDC.
参考答案:
【答案】
(1)解:如图,线段BD为所求出;

(2)证明:∵∠A=36°,AB=AC,
∴∠ABC=∠C= ![]() (180°﹣36°)=72°.
(180°﹣36°)=72°.
∵BD平分∠ABC,
∴∠ABD=∠DBC=72°÷2=36°.
∵∠A=∠CBD=36°,∠C=∠C,
∴△ABD∽△BDC.
【解析】(1)利用角平分线的作法作出线段BD即可;(2)先根据等腰三角形的性质得出∠ABC=∠C=72°,再由角平分线的性质得出∠ABD的度数,故可得出∠A=∠CBD=36°,∠C=∠C,据此可得出结论.
【考点精析】本题主要考查了等腰三角形的性质和相似三角形的判定的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1 , 弧K1K2 , 弧K2K3 , 弧K3K4 , 弧K4K5 , 弧K5K6 , …的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1 , L2 , L3 , L4 , L5 , L6 , ….当AB=1时,L2016等于( )
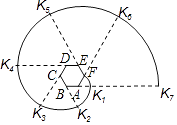
A.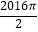
B.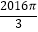
C.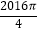
D.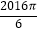 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3.14﹣π)0+|1﹣
 |+(﹣
|+(﹣  )﹣1﹣2sin60°.
)﹣1﹣2sin60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了改善办学条件,计划购置一批实物投影仪和一批台式电脑,经投标,购买1台实物投影仪和2台电脑共用了11000元;购买2台实物投影仪和3台电脑共用了18000元.
(1)求购买1台实物投影仪和1台电脑各需多少元?
(2)根据该校实际情况,需购买实物投影仪和台式电脑的总数为50台,要求购买的总费用不超过180000元,该校最多能购买多少台电脑? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.

(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,
 ).
). 
相关试题

