【题目】如图,直线![]() 过点A(0,6),点D(8,0),直线
过点A(0,6),点D(8,0),直线![]() :
:![]() 与
与![]() 轴交于点C,两直线
轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)连接AC,求![]() 的面积;
的面积;
(3)若在AD上有一点P,把线段AD分成2:3的两部分时,请直接写出点P的坐标(不必写解答过程).

参考答案:
【答案】(1)直线![]() 的解析式为
的解析式为![]() ,
,![]() ;(2)15;(3)点P的坐标为
;(2)15;(3)点P的坐标为![]() 或
或![]() .
.
【解析】
(1)先利用待定系数法可求出直线![]() 的解析式,再联立直线
的解析式,再联立直线![]() ,
,![]() 的解析式可得点B的坐标;
的解析式可得点B的坐标;
(2)先根据直线![]() 的解析式求出点C的坐标,再根据点
的解析式求出点C的坐标,再根据点![]() 的坐标分别求出
的坐标分别求出![]() 的长以及点B到x轴的距离,然后根据
的长以及点B到x轴的距离,然后根据![]() 的面积等于
的面积等于![]() 的面积减去
的面积减去![]() 的面积即可得;
的面积即可得;
(3)设点P的坐标为![]() ,先利用两点之间的距离公式求出AD的长,再根据题意可得
,先利用两点之间的距离公式求出AD的长,再根据题意可得![]() 或
或![]() ,然后利用两点之间的距离公式分别列出等式,求解即可得.
,然后利用两点之间的距离公式分别列出等式,求解即可得.
(1)设直线![]() 的解析式为
的解析式为![]()
∵直线![]() 经过
经过![]()
∴将点![]() 代入解析式得:
代入解析式得:![]()
解得
则直线![]() 的解析式为
的解析式为![]()
联立![]() ,
,![]() 的解析式得:
的解析式得:
解得![]()
则点B的坐标为![]() ;
;
(2)对于直线![]() :
:![]()
当![]() 时,
时,![]() ,解得
,解得![]()
则点C的坐标为![]()
![]()
![]() ,点B到x轴的距离为3
,点B到x轴的距离为3
则![]()
![]()
![]()
即![]() 的面积为15;
的面积为15;
(3)由题意,设点P的坐标为![]() ,且
,且![]()
![]()
![]()
![]() 点P把线段AD分成
点P把线段AD分成![]() 的两部分
的两部分
![]() 或
或![]()
①当![]() 时
时
由两点之间的距离公式得:![]()
解得![]()
![]()
则此时点P的坐标为![]()
②当![]() 时
时
由两点之间的距离公式得:![]()
解得![]()
![]()
则此时点P的坐标为![]()
综上,点P的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应集合的括号内
+8.5, 0, -3.4, 12, -9,
 , 3.1415, -1.2,
, 3.1415, -1.2, ,
, 
(1)正数集合 { }
(2)整数集合 { }
(3)负分数集合 { }
(4)非正整数集合{ }
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……,按此规律第5个图中共有点的个数是( )

A. 31 B. 46 C. 51 D. 66
-
科目: 来源: 题型:
查看答案和解析>>【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买
 个文具盒,10件奖品共需
个文具盒,10件奖品共需 元,求
元,求 与
与 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题(1)-100 + 80;
(2)(-18)÷4;
(3)
 ;
;(4)﹣7.2﹣0.8﹣5.6+11.6
(5)
 ;
;(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点A、B,分别用a,b表示,那么A、B两点之间的距离为:AB=|a-b|.利用此结论,回答以下问题:
(1)数轴上表示2和5的两点的距离是 ,数轴上表示-20和-5的两点之间的距离是 ,数轴上表示15和-30的两点之间的距离是 .
(2)数轴上表示x和-1的两点A,B之间的距离是 ,如果|AB|=2,那么x是
(3)式子|x+1|+|x-2|+|x-3|的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并回答问题:
三峡之最
三峡工程是中国,也是世界上最大的水利枢纽工程,是治理和开发长江的关键性骨干工程.它具有防洪、发电、航运等综合效益.
三峡水库总库容
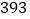 亿立方米,防洪库容
亿立方米,防洪库容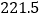 亿立方米,水库调洪可消减洪峰流量达每秒
亿立方米,水库调洪可消减洪峰流量达每秒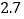 ─
─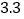 万立方米,是世界上防洪效益最为显著的水利工程.
万立方米,是世界上防洪效益最为显著的水利工程.三峡水电站总装机
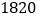 万千瓦,年发电量
万千瓦,年发电量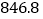 亿千瓦.时,是世界上最大的电站.
亿千瓦.时,是世界上最大的电站.三峡水库回水可改善川江
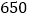 公里的航道,使宜渝船队吨位由现在的
公里的航道,使宜渝船队吨位由现在的 吨级堤高到万吨级,年单向通过能力由
吨级堤高到万吨级,年单向通过能力由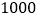 万吨增加到
万吨增加到 万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.思考:
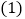 三峡水电站年发电量
三峡水电站年发电量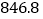 亿千瓦.时,一个普通家庭一天用电
亿千瓦.时,一个普通家庭一天用电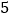 千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留
千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留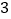 个有效数字)
个有效数字) 宜都市
宜都市 万人,平均一户
万人,平均一户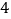 个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
相关试题

