【题目】某农户承包果树若干亩,今年投资![]() 元,收获水果总产量为
元,收获水果总产量为![]() 千克.此水果在市场上每千克售
千克.此水果在市场上每千克售![]() 元,在果园直接销售每千克售
元,在果园直接销售每千克售![]() 元
元![]() .该农户将水果拉到市场出售平均每天出售
.该农户将水果拉到市场出售平均每天出售![]() 千克,需
千克,需![]() 人帮忙,每人每天付工资
人帮忙,每人每天付工资![]() 元,农用车运费及其他各项税费平均每天
元,农用车运费及其他各项税费平均每天![]() 元.
元.
![]() 分别用含
分别用含![]() ,
,![]() 的代数式表示两种方式出售水果的收入.
的代数式表示两种方式出售水果的收入.
![]() 若
若![]() 元,
元,![]() 元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
![]() 该农户加强果园管理,力争到明年纯收入达到
该农户加强果园管理,力争到明年纯收入达到![]() 元,而且该农户采用了
元,而且该农户采用了![]() 中较好的出售方式出售,那么纯收入增长率是多少(纯收入
中较好的出售方式出售,那么纯收入增长率是多少(纯收入![]() 总收入-总支出)?
总收入-总支出)?
参考答案:
【答案】(1) 市场上出售收入为:![]() 元,果园直接出售收入为
元,果园直接出售收入为![]() 元;(2)应选择在市场出售,理由见解析;(3)长率为
元;(2)应选择在市场出售,理由见解析;(3)长率为![]()
【解析】
![]() 市场出售收入=水果总收入-额外支出,而水果直接在果园的出售收入为
市场出售收入=水果总收入-额外支出,而水果直接在果园的出售收入为![]() ;
;
![]() 根据
根据![]() 中得到的代数式,将
中得到的代数式,将![]() ,
,![]() 代入代数式计算即可.
代入代数式计算即可.
![]() 根据
根据![]() 的数据,首先确定今年的最高收入,然后计算增长率即可.
的数据,首先确定今年的最高收入,然后计算增长率即可.
解:![]() 将这批水果拉到市场上出售收入为:
将这批水果拉到市场上出售收入为:
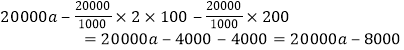 (元)
(元)
在果园直接出售收入为![]() 元;
元;
![]() 当
当![]() 时,市场收入为
时,市场收入为![]() (元).
(元).
当![]() 时,果园收入为
时,果园收入为![]() (元).
(元).
因为![]() ,所以应选择在市场出售;
,所以应选择在市场出售;
![]() 因为今年的纯收入为
因为今年的纯收入为![]() ,
,![]() ,
,
所以增长率为![]() .
.
-
科目: 来源: 题型:
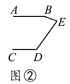
查看答案和解析>>【题目】有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从图②③④中,选一个说明它成立的理由.
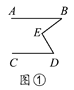
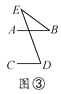
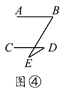
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
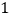 是一个长为
是一个长为 、宽为
、宽为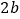 的长方形(其中
的长方形(其中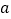 ,
,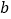 均为正数,且
均为正数,且 ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图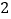 方式拼成一个大正方形.
方式拼成一个大正方形.如图
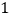 是一个长为
是一个长为 、宽为
、宽为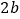 的长方形(其中
的长方形(其中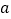 ,
,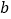 均为正数,且
均为正数,且 ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图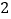 方式拼成一个大正方形.
方式拼成一个大正方形. 你认为图
你认为图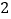 中大正方形的边长为________;小正方形(阴影部分)的边长为________.(用含
中大正方形的边长为________;小正方形(阴影部分)的边长为________.(用含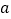 、
、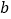 的代数式表示)
的代数式表示) 仔细观察图
仔细观察图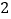 ,请你写出下列三个代数式:
,请你写出下列三个代数式: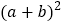 ,
,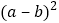 ,
,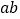 所表示的图形面积之间的相等关系,并选取适合
所表示的图形面积之间的相等关系,并选取适合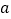 、
、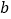 的数值加以验证.
的数值加以验证.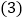 已知
已知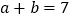 ,
,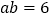 .求代数式
.求代数式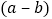 的值.
的值.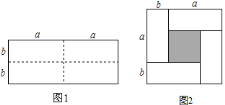
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=﹣
 x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA. 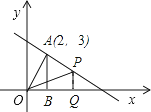
(1)求此一次函数的解析式;
(2)设点P为直线y=﹣ x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ=
x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ=  S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,距小明家楼下D点20米的B处有一根废弃的电线杆AB,经测得此电线杆与水平线DB所成锐角为60°,在小明家楼顶C处测得电线杆顶端A的俯角为30°,底部点B的俯角为45°(点A、B、D、C在同一平面内).已知在以点B为圆心,10米长为半径的圆形区域外是一休闲广场,有关部门想把此电线杆水平放倒,且B点不动,为安全起见,他们想知道这根电线杆放倒后,顶端A能否落在休闲广场内?请通过计算回答.
(结果精确到0.1米,参考数据: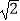 ≈1.414,
≈1.414, 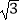 ≈1.732)
≈1.732)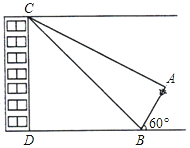
-
科目: 来源: 题型:
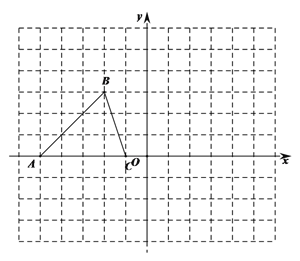
查看答案和解析>>【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
(1)画出△ABC关于坐标原点O成中心对称的△A1B1C1;
(2)将△ABC绕坐标原点O顺时针旋转90°,画出对应的△A′B′C′,
(3)若以A′、B′、C′、D′为顶点的四边形为平行四边形,请直接写出在第四象限中的D′坐标 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,延长弦BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
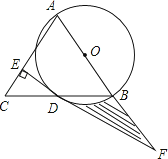
(1)判断直线DE与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为6,∠BAC=60°,延长ED交AB延长线于点F,求阴影部分的面积.
相关试题

