Question

【题目】如图1是一个五角星.

（1）计算：∠A+∠B+∠C+∠D+∠E的度数．

（2）当BE向上移动，过点A时，如图2，五个角的和（即∠CAD+∠B+∠C+∠D+∠E）有无变化？说明你的理由．

（3）如图3，把图2中的点C向上移到BD上时，五个角的和(即∠CAD＋∠B＋∠ACE＋∠D＋∠E)有无变化?说明你的理由．

Answer 1

【答案】：； 不变，; 理由见解析.（3）无变化．理由见解析.

【解析】

（1）运用三角形的内角和定理求解；

（2）利用三角形的外角等于与它不相邻的两内角之和求解；

（3）把五个角转化为一个平角求解即可

（1）AC与BE相交于点H，AD与BE相交于点G，如图，

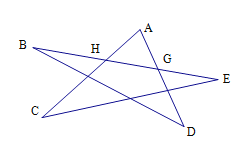
∵∠AHG是△HCE的外角，

∴∠AHG=∠C+∠E，

∵∠AGH是△GBD的外角，

∴∠AGH=∠B+∠D，

∵∠A+∠AHG+∠AGH=180，

∴∠A+∠B+∠C+∠D+∠E=180°；

（2）不变，

∠CAD+∠B+∠ACE+∠D+∠E=180°．

理由：由三角形的外角性质，知∠BAC=∠E+∠ACE，∠EAD=∠B+∠D，

∴∠C+∠E+∠CAD+∠B+∠D=180°，

即∠CAD+∠B+∠C+∠D+∠E=180°．

（3）无变化．

∵∠ACB=∠CAD+∠D，∠ECD=∠B+∠E，

∴∠CAD+∠B+∠ACE+∠D+∠E

=∠ACB+∠ACE+∠ECD

=180°.