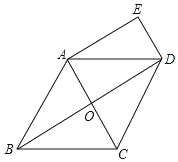
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若△ABC是边长为2的正三角形,求四边形AODE的面积.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意可判断出四边形AODE是平行四边形,再由菱形的性质可得出AC⊥BD,即∠AOD=90°,继而可判断出四边形AODE是矩形.
(2)由菱形的性质和勾股定理求出OB,得出OD,由矩形的性质即可得出答案.
(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=∠AOD=90°,
∴四边形AODE是矩形;
(2)∵△ABC是边长为2的正三角形,
∴AB=AC=2,
∠ABC=60°,
∵四边形ABCD为菱形,
∴AO=![]() AC=1,OD=OB,
AC=1,OD=OB,
∵∠AOB=90°,
∴OB=![]()
∴OD=OB=![]() ,
,
∵四边形AODE是矩形,
∴四边形AODE的面积=![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
-
科目: 来源: 题型:
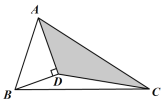
查看答案和解析>>【题目】如图,AD平分∠BAC,BD⊥AD,垂足为D,连接CD,若三角形△ABC内有一点P,则点P落在△ADC内(包括边界的阴影部分)的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC的中点,DE∥AB交AC于点E,∠B=34°.
(1)求∠BAD的度数;
(2)求证:AE=DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知:点A(0,0),B(
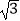 ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 .
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, 的平分线交
的平分线交 于点E,交
于点E,交 的延长线于F,以
的延长线于F,以 为邻边作平行四边形
为邻边作平行四边形 。
。(1)证明平行四边形
 是菱形;
是菱形;(2)若
 ,连结
,连结 ,①求证:
,①求证: ;②求
;②求 的度数;
的度数;(3)若
 ,
, ,
, ,M是
,M是 的中点,求
的中点,求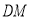 的长。
的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN//EF, 点C 为两直线之间一点,若∠CAM 的平分线与∠CBF 的平分线所在的直线相交于点 D ,则∠ACB与 ∠ADB 之间的数量关系是 .

相关试题

