【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示) 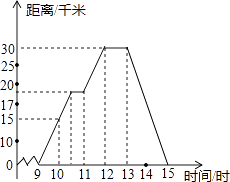
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
参考答案:
【答案】
(1)解:由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)解:由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)解:由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)解:由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30﹣19=11(千米);
(5)解:由纵坐标看出12:00﹣13:00时距离没变且时间较长,得12:00﹣13:00休息并吃午饭;
(6)解:由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时).
【解析】(1)根据函数图象,可得自变量、因变量;(2)根据函数图象的纵坐标,可得答案;(3)根据函数图象的横坐标、纵坐标,可得答案;(4)根据函数图象的横坐标,可得函数值,根据函数值相减,可得答案;(5)根据函数图象的纵坐标,可得答案;(6)根据函数图象的纵坐标,可得距离,根据函数图象的横坐标,可得时间,根据路程除以时间,可得答案.
【考点精析】关于本题考查的函数的图象,需要了解函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中秋节前夕,旺客隆超市采购了一批土特产,根据以往销售经验,每天的售价与销售量之间有如下表的关系:

设当售价从38元/千克下调到x元/千克时,销售量为y千克.
(1)根据上述表格中提供的数据,通过在直角坐标系中描点、连线等方法,猜测并求出y与x之间的函数表达式;
(2)如果这种土特产的成本价是20元/千克,为使某一天的利润为780元,那么这一天每千克的售价应为多少元?(利润=销售总金额-成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价是500元,标价是700元,商店要求以不低于5%的利润率打折出售,售货员最低可以打_________折.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲地的海拔高度是h m,乙地的海拔高度是甲地海拔高度的3倍多20m,丙地的海拔高度比甲地的海拔高度低30m,列式计算乙、丙两地的高度差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
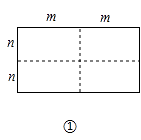
(1)图②中的阴影部分的正方形边长为;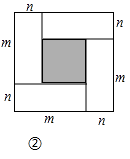
(2)观察图②,三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系是;
(3)观察图③,你能得到怎样的代数恒等式呢?;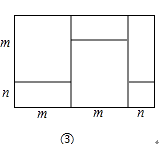
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+2n)=m2+3mn+2n2 . (画在虚线框内) -
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是(写成两数平方差的形式);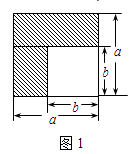
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 , 长是 , 面积是 . (写成多项式乘法的形式)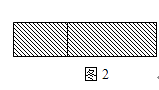
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 . (用式子表达)
(4)运用你所得到的公式,计算下列各题: ①10.3×9.7
②(2m+n﹣p)(2m﹣n+p) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算a6a2的结果是( )
A. a12 B. a8 C. a4 D. a3
相关试题

