【题目】若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

参考答案:
【答案】(1)2.
(2)t=10s,15s,20s.
【解析】
(1)根据好点定义可列方程,x-(-2)=2×(4-x),从而得出结论;
(2)分四种情况讨论,由好点定义可列方程,即可求解;
解:(1)设这个点表示的数为x,
∴x-(-2)=2×(4-x)
解得:x=2
故答案为2
(2)当点P是【A,B】的好点
∴60-2t=2×2t
解得:t=10
当点P是【B,A】的好点
∴2(60-2t)=2t
解得:t=20
当点A是【B,P】的好点
∴60=2×(60-2t)
解得:t=15
点B是【A,P】的好点
∴60=2×2t
解得:t=15
综上所述:t=10s,15s,20s时,P、A和B中恰有一个点为其余两点的好点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(-1,y1),(2,y2),(3,y3)在反比例函数
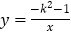 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )A. y1>y2>y3 B. y1>y3>y2 C. y3>y1>y2 D. y2>y3>y1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个关于是否成反比例的命题,判断它们的真假.
(1)面积一定的等腰三角形的底边长和底边上的高成反比例;
(2)面积一定的菱形的两条对角线长成反比例;
(3)面积一定的矩形的两条对角线长成反比例;
(4)面积一定的直角三角形的两直角边长成比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB=4
 ,AC⊥AB,BD⊥AB,AC=BD=3
,AC⊥AB,BD⊥AB,AC=BD=3 .点 P 在线段 AB 上以 1
.点 P 在线段 AB 上以 1 的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为
的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为  (s).
(s).(1)若点 Q 的运动速度与点 P 的运动速度相等,当
 =1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;
=1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点 Q 的运动速度为

 ,是否存在实数
,是否存在实数 ,使得△ACP 与△BPQ 全等?若存在,求出相应的
,使得△ACP 与△BPQ 全等?若存在,求出相应的 、
、 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论的有__________.(把正确结论的序号都写上去)

-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.
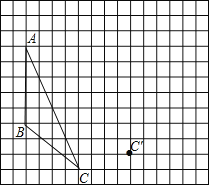
(1)请画出平移后的△A'B'C';
(2)若连接AA',BB',则这两条线段的关系是 ;
(3)利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE;
(4)线段AB在平移过程中扫过区域的面积为 .
相关试题

