【题目】问题情境:如图,已知AB∥CD,∠1=∠2,求证:∠3=∠4.

解法展示:证明:延长BE交直线CD于点M,如图所示.

∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是_____________,根据4是____________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
参考答案:
【答案】(1)两直线平行,内错角相等 ; 等量代换 ; 同位角相等,两直线平行 ; 两直线平行,内错角相等;(2)已知:①③,求证:②;是真命题,见解析.
【解析】
延长BE交直线CD于点M,利用平行线的性质和判定定理进行证明即可.
解:(1)证明:延长BE交直线CD于点M,如图所示.
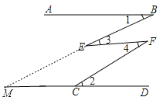
∵AB∥CD,∴∠1=∠BMC(两直线平行,内错角相等).
∵∠1=∠2,∴∠2=∠BMC(等量代换).
∴BE∥CF(同位角相等,两直线平行).
∴∠3=∠4(两直线平行,内错角相等).
故答案为:两直线平行,内错角相等;等量代换; 同位角相等,两直线平行; 两直线平行,内错角相等.
(2)交换①和③或交换②和③都是真命题.选择交换②和③,成为新命题.
已知:①③,求证:②.
理由:如图,延长BE交直线CD于点M.

∵∠3=∠4,
∴BE∥CF.
∴∠2=∠BMC.
∵AB∥CD,
∴∠1=∠BMC
.∴∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 (如图),点
(如图),点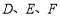 分别在边
分别在边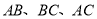 上,且四边形
上,且四边形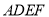 是菱形
是菱形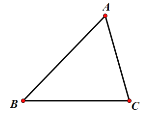
(1)请使用直尺与圆规,分别确定点
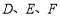 的具体位置(不写作法,保留画图痕迹);
的具体位置(不写作法,保留画图痕迹);(2)如果
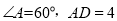 ,点
,点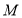 在边
在边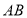 上,且满足
上,且满足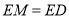 ,求四边形
,求四边形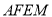 的面积;
的面积;(3)当
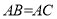 时,求
时,求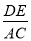 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则
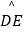 的长为( )
的长为( )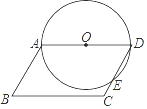
A. π
π
B. π
π
C. π
π
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程
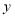 (米)与行驶时间
(米)与行驶时间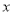 (分钟)的变化关系
(分钟)的变化关系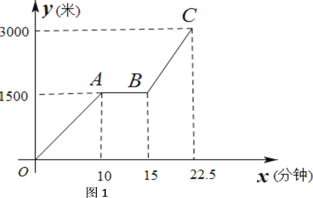
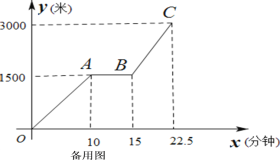
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是
 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )

A.
B.2
C.
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )
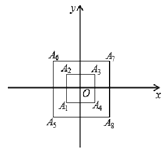
A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】五子棋深受广大棋友的喜爱,其规则是:在 15 15 的正方形棋盘中,由黑方先行,轮流奕子,在任何一方向(横向、竖向或斜线 方向)上连成五子者为胜。如图 3 是两个五子棋爱好者甲和乙的 部分对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若 A 点的位置记作(8,4),若不让乙在短时间内获胜,则甲必须落子 的位置是___________.

相关试题

