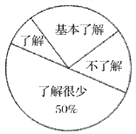
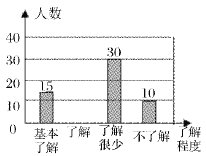
【题目】“食品安全”受到全社会的广泛关注,我市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
扇形统计图 条形统计图
参考答案:
【答案】 60 90 (2) 300人
【解析】分析:(1)由了解很少的有30人,占50%,可求得接受问卷调查的学生数,继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角;
(2)由(1)可求得了解的人数,继而补全条形统计图;
(3)利用样本估计总体的方法,即可求得答案.
详解:(1)∵了解很少的有30人,占50%,∴接受问卷调查的学生共有:30÷50%=60(人);
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:![]() ×360°=90°;
×360°=90°;
故答案为:60,90;
(2)60﹣15﹣30﹣10=5;
补全条形统计图得:
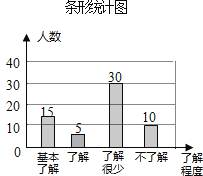
(3)根据题意得:900×![]() =300(人),则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人.
=300(人),则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人.
-
科目: 来源: 题型:
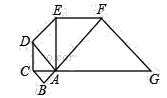
查看答案和解析>>【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=12 cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点.
(1)若点C恰好是AB中点,则DE=_____cm.
(2)若AC=4 cm,求DE的长;
(3)试利用“字母代替数”的方法,说明不论AC取何值(不超过12 cm),DE的长不变;
(4)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.
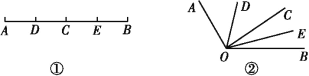
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图,若点A.O.B在一条直线上,则∠AOB与∠EOF的数量关系是:∠AOB=_____∠EOF.
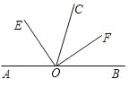
(2)如图,若点A.O.B不在一条直线上,则题(1)中的数量关系是否成立?请说明理由.
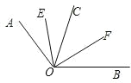
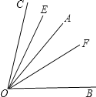
(3)如图,若OA在∠BOC的内部,则题(1)中的数量关系是否仍成立?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径作
 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.(1)求证: EF与
 相切;
相切;(2)若AE=6,
 ,求EB的长.
,求EB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD.
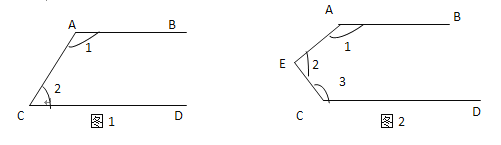
(1)则图①中的∠1+∠2的度数是180°.
(2)则图②中的∠1+∠2+∠3的度数是多少?
解:如图⑤,过点E作EF∥AB(为了解题的需要,添加的线叫做辅助线,辅助线常常画成虚线).
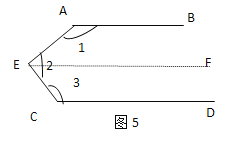
所以∠1+∠AEF=180°.
因为AB∥CD,
所以CD∥EF.
所以∠FEC+∠3=180°.
所以∠1+∠2+∠3=360°.
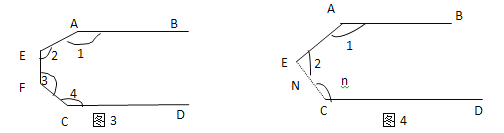
认真阅读(2)的解题过程,求图③中∠1+∠2+∠3+∠4的度数是多少?探究图④中∠1+∠2+∠3+∠4+…+∠n的度数是多少?
-
科目: 来源: 题型:
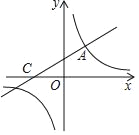
查看答案和解析>>【题目】如图,直线
 与双曲线
与双曲线 相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C.(1)求双曲线的解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
相关试题

