【题目】阅读下面材料:
数学课上,老师让同学们解答课本中的习题:如图1,在四边形ABCD中,E、F、
G、H分别是各边的中点,猜想四边形EFGH的形状并证明自己的猜想.
小丽在思考问题时,有如下思路:连接AC
结合小丽的思路作答:
(1)若只改变图1中的四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?请说明理由
参考小丽思考问题方法,解决以下问题:
(2)如图2,在(1)的条件下,若连接AC、BD
①当AC与BD满足什么关系时,四边形EFGH是菱形.写出结论并证明.
②当AC与BD满足什么关系时,四边形EFGH是正方形.直接写出结论
参考答案:
【答案】
(1)解:结论:四边形EFGH还是平行四边形.
理由:如图2,连接AC.

∵E、F分别是AB、CB中点
∴EF∥AC,EF= ![]() AC,
AC,
同理:GH∥AC,GH= ![]() AC,
AC,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形
(2)解:①结论:当AC=BD时,四边形EFGH是菱形.
理由:如图3中,由(1)四边形EFGH是平行四边形
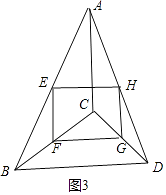
∵E、F是AB、CB中点
∴EF= ![]() AC
AC
同理:EH= ![]() BD
BD
∵AC=BD
∴EF=EH
∴平行四边形EFGH是菱形.
②结论:当AC⊥BD且AC=BD时,四边形EFGH是正方形.
理由:由①可知,AC=BD,四边形EFGH是菱形,
∵AC⊥BD,AC∥HG,
∴HG⊥BD,
∵EH∥BD,
∴EH⊥HG,
∴∴∠EHG=90°,
∴四边形EFGH是正方形
【解析】(1)结论:四边形EFGH还是平行四边形.只要证明EF=GH,EF∥GH即可;(2)①利用(1)的结论,只要证明EF=EH即可;②在①基础上,只要证明∠EHG=90°即可;
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在 Rt△ABC中,∠C=90°,AD 平分∠BAC交BC于D,若 BC=20,且BD:DC=3:2,则D到AB边的距离是( )
A. 12 B. 10 C. 8 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证:
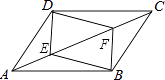
(1)DE=BF;
(2)四边形DEBF是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).

(1)求原有蓄水量y1(万m3)与时间x(天)的函数关系式,并求当x=20时的水库总蓄水量.
(2)求当0≤x≤60时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x的范围),若总蓄水量不多于900万m3为严重干旱,直接写出发生严重干旱时x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人在跳远练习中,6次成绩分别为(单位:米): 甲:3.8 3.8 3.9 3.9 4.0 4.0; 乙:3.8 3.9 3.9 3.9 3.9 4.0.
则这次跳远练习中,甲乙两人成绩方差的大小关系是( )
A.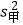 >
> 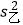
B.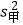 <
< 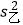
C.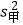 =
= 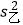
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a-b=9,ab=-14,则a2+b2的值为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+m=0有实数根,则m的取值范围是 .
相关试题

