【题目】如图,在ABCD中,E,F分别为边AD,BC的中点,对角线AC分别交BE,DF于点G,H.求证:AG=CH.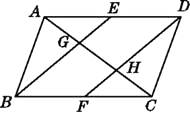
参考答案:
【答案】证明:∵E,F分别是AD,BC的中点,
∴AE=DE= ![]() AD,CF=BF=
AD,CF=BF= ![]() BC.
BC.
又∵AD∥BC,且AD=BC.
∴DE∥BF,DE=BF,AE=CF.
∴四边形BEDF是平行四边形.
∴∠BED=∠DFB.
∴∠AEG=∠CFH.
又∵AD∥BC,∴∠EAG=∠FCH.
在△AGE和△CHF中,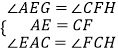
∴△AGE≌△CHF.
∴AG=CH.
【解析】先根据已知条件易证明四边形BEDF是平行四边形得出∠BED=∠DFB,再根据等角的补角相等及平行线的性质证明∠AEG=∠CFH,∠EAG=∠FCH,然后证明△AGE≌△CHF,根据全等三角形的性质即可证得结论。
-
科目: 来源: 题型:
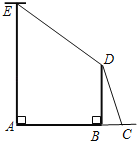
查看答案和解析>>【题目】如图,AE是位于公路边的电线杆,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根水泥撑杆BD,用于撑起拉线.已知公路的宽AB为8米,电线杆AE的高为12米,水泥撑杆BD高为6米,拉线CD与水平线AC的夹角为67.4°.求拉线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).(参考数据:sin67.4°≈
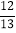 ,cos67.4°≈
,cos67.4°≈ ,tan67.4°≈
,tan67.4°≈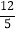 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数的平方根是a+3和2a﹣15,那么这个数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个图象经过第一、三象限的正比例函数的解析式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线向左平移2个单位,再向下平移3个单位后,所得抛物线的解析式为y=x2﹣1,则原抛物线的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某商店的一支圆珠笔比一支铅笔贵1元,三支圆珠笔与两支铅笔共卖18元,那么在这家商店用14元恰好买这两种笔共____支.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD及等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:
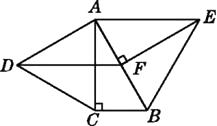
(1)AC=EF;
(2)四边形ADFE是平行四边形.
相关试题

