【题目】(2016·西宁中考)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() ,求BE的长.
,求BE的长.

参考答案:
【答案】(1)见解析 (2)![]()
【解析】试题分析:(1)连OD,由AB是⊙O的直径,根据圆周角定理得到∠ADO+∠ODB=90°,而∠CDA=∠CBD,∠CBD=∠ODB,于是∠CDA+∠ADO=90°,根据切线的判定即可得证;
(2)根据已知条件得到△CDA∽△CBD由相似三角形的性质得到![]() ,求得CD=4,由切线长定理得到BE=DE,BE⊥BC,在Rt△CBE中根据勾股定理列方程即可得到结论.
,求得CD=4,由切线长定理得到BE=DE,BE⊥BC,在Rt△CBE中根据勾股定理列方程即可得到结论.
试题解析:(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD.
∵OD是⊙O的半径,
∴CD是⊙O的切线;

(2)解:∵∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD,
∴![]() =
=![]() .
.
∵![]() =
=![]() ,BC=6,
,BC=6,
∴CD=4.
∵CE,BE是⊙O的切线,
∴BE=DE,BE⊥BC,
∴BE2+BC2=EC2,
即BE2+62=(4+BE)2,
解得BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一根长1m的木尺,共有9个等分点,每个分点处有折痕,可将木尺折断,现欲将木尺折成3节,并使3节能组成三角形,若要组成形状不同的三角形,共有多少种不同的折法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若规定向东走为正,那么﹣8米表示( )
A.向东走8米
B.向南走8米
C.向西走8米
D.向北走8米 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.4x2y﹣xy2=3x2y
B.3(x﹣1)=3x﹣1
C.﹣3a+7a+1=﹣10a+1
D.﹣(x﹣6)=﹣x+6 -
科目: 来源: 题型:
查看答案和解析>>【题目】(中考·安徽)如图,已知反比例函数y=
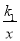 与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=
 的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的个数有( )
⑴零是最小的整数;
⑵正数和负数统称为有理数;
⑶|a|总是正数;
⑷﹣a表示负数.
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知空气的单位体积质量是0.01239g/cm3 , 数据0.001239用科学记数法可表示为( )
A.1.239×10﹣3
B.1.239×10﹣2
C.0.1239×10﹣2
D.12.39×10﹣4
相关试题

