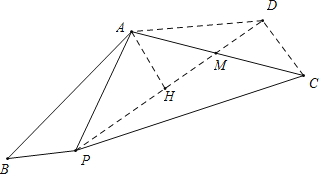
【题目】如图，线段AB绕着点A逆时针方向旋转120°得到线段AC，点B对应点C，在∠BAC的内部有一点P，PA＝8，PB＝4，PC＝4，则线段AB的长为_____．

【答案】4

【解析】

将△ABP绕点A逆时针旋转120°，得到△ACD，连接PD，过点A作AH⊥PD于H，利用等腰三角形的性质及通过解直角三角形求出AH，PH，DH，PD的长，利用勾股定理的逆定理证明△PDC为直角三角形，再证△DMC∽△HMA，其对应边相等，可推出AM＝CM＝AC，HM＝DM＝HD＝2，在Rt△DMC中，通过勾股定理求出CM的长，可推出AB＝AC＝2CM＝4．

如图，将△ABP绕点A逆时针旋转120°，得到△ACD，连接PD，过点A作AH⊥PD于H，

则△ABP≌△ACD，∠PAD＝120°，

∴PA＝DA＝8，PB＝DC＝4，∠APH＝∠ADH＝30°，

∴AH＝AP＝4，

∴PH＝DH＝=4，

∴PD＝2PH＝8，

在△PDC中，

PD2+CD2＝(8)2+42＝208，

PC2＝(4)2＝208，

∴PD2+CD2＝PC2，

∴△PDC为直角三角形，且∠PDC＝90°，

∴∠AHD＝∠PDC，

∴AH∥DC，

∴△DMC∽△HMA，

∵DC＝AH＝4，

∴AM＝CM＝AC，HM＝DM＝HD＝2，

∴在Rt△DMC中，

CM＝＝2，

∴AB＝AC＝2CM＝4，

故答案为：4．

关闭