【题目】如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.

(1)求直线l所表示的一次函数的表达式;
(2)若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3.请判断点P3是否在直线l上,并说明理由.
参考答案:
【答案】(1) y=2x﹣3;(2) 点P3在直线l上.
【解析】
本题考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征以及一次函数图象的几何变换.在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
解:(1)设直线l所表示的一次函数的表达式为y=kx+b(k≠0),
∵点P1(2,1),P2(3,3)在直线l上,
∴![]() , 解得
, 解得![]() .
.
∴直线l所表示的一次函数的表达式为y=2x﹣3.
(2)点P3在直线l上.
由题意知点P3的坐标为(6,9),
∵2×6﹣3=9, ∴点P3在直线l上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
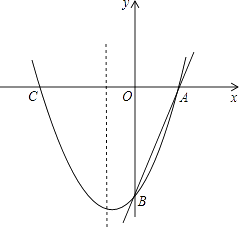
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为  m.
m. 
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
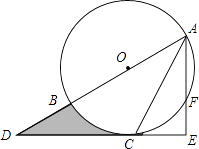
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3)

(1)求此二次函数的解析式和顶点坐标;
(2)直线y2=kx+b过B、C两点,请直接写出当y1>y2时,自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE:CD=5:24

(1)求CD的长;
(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

①以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1;
②将△ABC绕A点逆时针旋转90°得到△AB2C2 , 画出△AB2C2 , 并求出AC扫过的面积.
相关试题

