【题目】如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.

(1)若点P、Q同时向右运动2秒,则点P表示的数为_______,点P、Q之间的距离是______个单位;
(2)经过__________秒后,点P、Q重合;
(3)试探究:经过多少秒后,点P、Q两点间的距离为14个单位.
参考答案:
【答案】(1)4,10(2)4,12(3)①![]() ②26③2
②26③2
【解析】试题分析:(1)点P表示的数为根据数在数轴的移动列算式计算即可. 点P、Q之间的距离是先求出移动后P、Q表示的数再相减即可.
(2)运动问题分为相遇和追及两种情况,分别列方程求出即可.
相遇:P的路程+Q的路程=PQ;追及P的路程-Q的路程=PQ
试题解析:(1)P表示的数:-8+2×2="-4," P表示的数:4+1×2=6 所以点P、Q之间的距离是6-(-4)= 10;
(2)设经t秒点P、Q重合 相遇时:2t+t=12解得t=4;追及时:2t-t=12解得t=12;
(3)P向左运动,Q向右运动时:①2t+t+12=14 解得 t=![]() .
.
点P、Q同时向左运动②2t=26+t 解得t=26
点P、Q同时向右运动 ③2t+12=14+t 解得t=2.
答:经过![]() 、26、2秒时,P、Q相距14个单位.
、26、2秒时,P、Q相距14个单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016四川省乐山市第21题)某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:

根据图表信息,回答下列问题:
(1)该班共有学生 人;表中a= ;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号里(将各数用逗号分开):﹣4,0.62,
 ,18,0,﹣8.91,+100
,18,0,﹣8.91,+100正数:{______…};负数:{______…};整数:{______…};分数:{______…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班数学学习小组某次测验成绩分别是63,72,70,49,66,81,53,92,69,则这组数据的极差是( )
A.47
B.43
C.34
D.29 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山东省泰安市第16题)如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
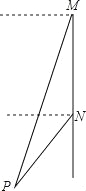
A.22.48 B.41.68 C.43.16 D.55.63
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山东省泰安市第18题)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )

A.44° B.66° C.88° D.92°
-
科目: 来源: 题型:
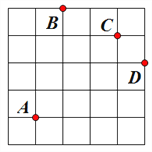
查看答案和解析>>【题目】如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息.
(1)图中B→D(______,______),C→______(+1,______);
(2)若甲虫A的爬行路线为A→B→C→D,计算甲虫A爬行的路程为 ;
(3)若甲虫A的爬行路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),最终到达甲虫P处,请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置.
相关试题

