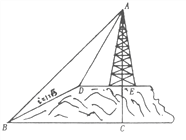
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
参考答案:
【答案】小山的高度为25米,铁架的高度为![]() 米.
米.
【解析】试题分析:
试题解析:(1)利用坡度先求出小三高度.(2) 证明△ADE≌△BDF全等,利用勾股定理求铁架的高度.
过D作DF⊥BC,交BC于点F,
∵小山的坡面坡度为1: ![]() ,即tan∠DBF=
,即tan∠DBF=![]() ,
,
∴∠DBF=30°,又∠ADE=60°,∠AED=90°,
∴∠DAE=30°,
∵∠CBA=∠CAB=45°,
∴∠CBA-∠DBF=∠CAB-∠DAE,即∠DAB=∠DBA,
∴DB=DA,
在△ADE和△BDF中,
∵∠DAE=∠DBF=30°,∠AED=∠BFD=90°,AD=BD,
∴△ADE≌△BDF(AAS),∴AE=BF,在Rt△BDF中,∠DBF=30°,BD=50米,
∴DF=0.5BD=25米,
根据勾股定理得:BF=![]() 米,则小山的高度为25米,铁架的高度为
米,则小山的高度为25米,铁架的高度为![]() 米.
米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合里.
-4,
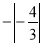 ,0,
,0, ,-3.14,717,-(+5),+1.88,
,-3.14,717,-(+5),+1.88,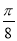
(1)正数集合:{ … };
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)分数集合:{ … }.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1和图2,在△ABC中,AB=13,BC=14,
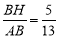 .
.探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积
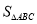 =___.
=___.拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为
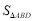 =0).
=0).(1)用含x、m或n的代数式表示
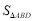 及
及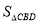 ;
;(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数3.3 ,-2 ,0 ,
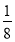 ,-3.5 ;
,-3.5 ;(1) 比较这些数的绝对值的大小,并将这些数的绝对值用“>”号连接起来;
(2) 比较这些数的相反数的大小,并将这些数的相反数用“<”号连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:关于x的二次函数
 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.
(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
 和y=﹣
和y=﹣ 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为_______.
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为_______.
相关试题

