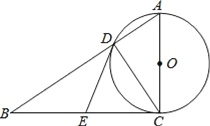
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2![]() ,则DE= ;
,则DE= ;
②当∠B= °时,以O,D,E,C为顶点的四边形是正方形.
参考答案:
【答案】(1)证明就解析;(2)①3;②45.
【解析】试题分析:(1)运用垂径定理、直角三角形的性质证明∠ODE=90°即可解决问题;
(2)①直接利用锐角三角函数关系得出BC的长,再利用直角三角形的性质得出DE的长;
②当∠B=45°时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
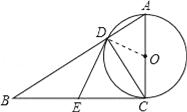
试题解析:(1)连接OD.
∵AC是直径,∴∠ADC=90°,∴∠CDB=90°,
又∵E为BC边的中点,∴DE为直角△DCB斜边的中线,∴DE=CE=![]() .∴∠DCE=∠CDE,
.∴∠DCE=∠CDE,
∵OC=OD,∴∠OCD=∠ODC,∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,∴∠ODE=90°
∴DE是⊙O的切线.
(2)①∵∠B=30°,AC=2![]() ,∠BCA=90°,∴tan30°=
,∠BCA=90°,∴tan30°=![]() =
=![]() ,解得:BC=6,
,解得:BC=6,
则DE=![]() BC=3;
BC=3;
故答案为:3;
②当∠B=45°时,四边形ODEC是正方形,
∵∠ACB=90°,∴∠A=45°,
∵OA=OD,∴∠ADO=45°,∴∠AOD=90°,∴∠DOC=90°,
∵∠ODE=90°,∴四边形DECO是矩形,
∵OD=OC,∴矩形DECO是正方形.
故答案为:45.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l外一点P与直线l上两点的连线段长分别为3cm,5cm,则点P到直线l的距离是( )
A. 不超过3cmB. 3cmC. 5cmD. 不少于5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于50棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算“※”:x※y=xy+x2﹣y2 , 化简(2a+3b)※(2a﹣3b),并求出当a=2,b=1时的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心,他们捐款的数额分别是(单位:元)50、20、50、30、25、50、55,这组数据的众数和中位数分别是( )
A.50元,30元
B.50元,40元
C.50元,50元
D.55元,50元 -
科目: 来源: 题型:
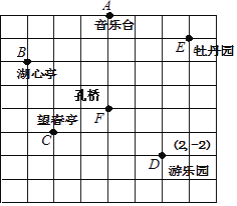
查看答案和解析>>【题目】王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,﹣2),请你帮她画出坐标系,并写出其他各景点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】元月份某天某市的最高气温是4℃,最低气温是-5℃,那么这天的温差(最高气温减最低气温)是______℃.
相关试题

