【题目】如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
参考答案:
【答案】
(1)解:四边形ABCD是矩形.理由如下:
∵AC与BD是圆的直径,
∴∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,
∴四边形ABCD是矩形;
(2)解:证明:∵BO=CO,
又∵BE⊥AC于E,CF⊥BD于F,
∴∠BEO=∠CFO=90°.
在△BOE和△COF中, 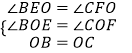 ,
,
∴△BOE≌△COF(AAS).
∴BE=CF.
【解析】(1)由圆周角定理得出∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,即可得出四边形ABCD是矩形;(2)由AAS证明△BOE≌△COF,得出对应边相等即可.
【考点精析】根据题目的已知条件,利用矩形的判定方法和圆周角定理的相关知识可以得到问题的答案,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=
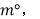 则∠BOE的度数是
则∠BOE的度数是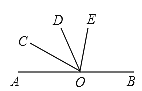
A.
 B.
B. 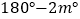 C.
C. 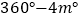 D.
D. 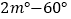
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级
 班数学课外兴趣小组在探究:“
班数学课外兴趣小组在探究:“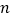 边形共有多少条对角线”这一问题时,设计了如下表格:
边形共有多少条对角线”这一问题时,设计了如下表格:多边形的边数
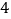
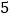
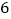
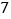
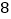
…
从多边形一个顶点出发可引起的对角线条数
…
多边形对角线的总条数
…
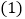 探究:假若你是该小组的成员,请把你研究的结果填入上表;
探究:假若你是该小组的成员,请把你研究的结果填入上表;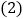 猜想:随着边数的增加,多边形对角线的条数会越来越多,从
猜想:随着边数的增加,多边形对角线的条数会越来越多,从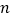 边形的一个顶点出发可引的对角线条数为多少,
边形的一个顶点出发可引的对角线条数为多少,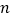 边形对角线的总条数为多少.
边形对角线的总条数为多少. 应用:
应用: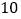 个人聚会,每不相邻的人都握一次手,共握多少次手?
个人聚会,每不相邻的人都握一次手,共握多少次手? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=3∠BOC,射线0D平分∠AOC,若∠BOD=30°,则∠BOC的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:
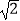 =1.41,
=1.41, 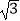 =1.73)
=1.73) 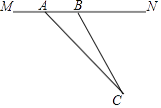
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则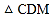 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
相关试题

