Question

【题目】如图，已知平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE，BF交于H，BF，AD的延长线交于G

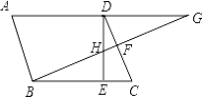
（1）求证：AB=BH

（2）若GA=10，HE=2,求AB的值

Answer 1

【答案】（1）证明见解析；（2）2．

【解析】

试题分析：（1）求出BE=DE，根据垂直推出∠CDE=∠HBE，证△BHE≌△DEC，推出BH=CD即可．

（2）根据AD∥BC推出三角形相似，得出比例式，求出BE的值，在△DEC中根据勾股定理求出CD即可．

试题解析：（1）∵DE⊥BC，BF⊥CD，

∴∠BEH=∠DEC=∠BFC=90°，

∴∠HBE+∠C=90°，∠CDE+∠C=90°，

∴∠HBE=∠CDE，

∵∠DBC=45°，∠DEB=90°，

∴∠BDE=45°=∠DBE，

∴BE=DE，

∵在△BHE和△DEC中

，

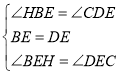∴△BHE≌△DEC，

∴BH=CD，

∵四边形ABCD是平行四边形，

∴AB=CD，

∴AB=BH．

（2）设BE=a，则BC=AD=a+2，DE=BE=a，DH=a-2，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴△DHG∽△EHB，

∴，

∵AG=10，

∴，

解得：a=4，

BE=DE=4，

在△DEC中，EC=EH=2，DE=4，由勾股定理得：CD=2，

∵四边形ABCD是平行四边形，

∴AB=CD=2．