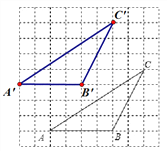
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
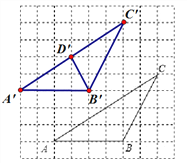
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

参考答案:
【答案】(1)画图见解析;(2)画图见解析;(3)平行且相等;(4)12;(5)9
【解析】试题分析:(1)利用网格特点和平移的性质分别画出点A、B、C的对应点A′、B′、C′即可得到△A′B′C′;
(2)找出线段A′C′的中点E′,连接B′E′;
(3)根据平移的性质求解;
(4)由于线段AB扫过的部分为平行四边形,则根据平行四边形的面积公式可求解.
(5)根据同底等高面积相等可知共有9个点.
试题解析:
(1)△A′B′C′如图所示;
(2)B′D′如图所示;
(3)BB′∥CC′,BB′=CC′;
(4)线段AB扫过的面积=4×3=12;
(5)有9个点.
-
科目: 来源: 题型:
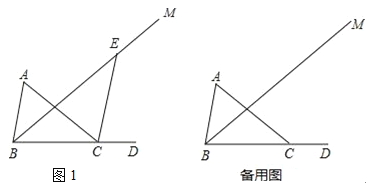
查看答案和解析>>【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个选项中,哪一个为多项式8x2-10x+2的因式( )
A.2x-2 B.2x+2
C.4x+1 D.4x+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
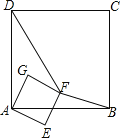
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
-
科目: 来源: 题型:
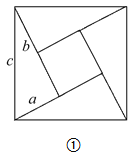
查看答案和解析>>【题目】如图所示,有四个同样大小的直角三角形,两条直角边分别为a,b,斜边为c,拼成一个正方形,中间留有一个小正方形.
(1)利用它们之间的面积关系,探索出关于a,b,c的等式.
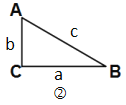
(2)利用(1)中发现的直角三角形中两直角边a,b和斜边c之间的关系,完成问题:如图,在直角△ABC中,∠C=90°,且c=6,a+b=8,则△ABC的面积为__________
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:
(1)
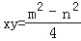 (2)x+y=m (3)x2﹣y2=mn
(2)x+y=m (3)x2﹣y2=mn(4)
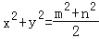 其中正确的有_________(填序号)
其中正确的有_________(填序号)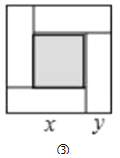
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四包真空包装的火腿肠,每包以标准质量450g为基准,超过的克数记作正数,不足的克数记作负数.下面的数据是记录结果,其中与标准质量最接近的是( )
A. +2 B. ﹣3 C. +4 D. ﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各题去括号所得结果正确的是( )
A. x2﹣(x﹣y+2z)=x2﹣x+y+2z B. x﹣(﹣2x+3y﹣1)=x+2x﹣3y+1
C. 3x﹣[5x﹣(x﹣1)]=3x﹣5x﹣x+1 D. (x﹣1)﹣(x2﹣2)=x﹣1﹣x2﹣2
相关试题

