【题目】(如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=2 ![]() .
. 
(1)求正方形ABCD的边长;
(2)求OE的长;
(3)①求证:CN=AF;②直接写出四边形AFBO的面积.
参考答案:
【答案】
(1)解:∵四边形ABCD是正方形,
∴AB=CD=BC,∠BCD=∠ABC=90°,
∴2BC2=BD2,
∵BD=2 ![]() ,
,
∴AB=BC=2,
∴正方形ABCD的边长为2
(2)解:∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,
∴∠AEC=∠CEF=90°,E为AF的中点,
∵正方形ABCD,
∴O为AC的中点,AC=BD=2 ![]() ,
,
∴OE= ![]() CF=
CF= ![]() BD=
BD= ![]()
(3)①证明:∠ABF=∠CBN=∠CEF=90°,AB=BC,
∴∠ECB+∠F=∠FAB+∠F=90°,
∴∠ECB=∠FAB,
在△NCB与△FAB中,
 ,
,
∴△NCB≌△FAB,
∴CN=AF.
②四边形AFBO的面积=△CBN的面积+△ABO的面积= ![]()
【解析】(1)利用正方形的性质和勾股定理计算即可;(2)利用正方形的性质解答即可;(3)判断出∠OEC=∠OCE,再判断出∠NBC=∠COM=90°,进而得出△CBN∽△COM,即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x0是方程ax2+2x+c=0(a≠0)的一个根,设M=1﹣ac,N=(ax0+1)2 , 则M与N的大小关系正确的为( )
A.M>N
B.M=N
C.M<N
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·苏州)有一组数据:2,5,5,6,7,这组数据的平均数为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】用大小相等的小正方形(阴影部分)按一定规律拼成下列图形,拼成第1个图形需要2个小正方形,拼第2个图形需要6个小正方形,拼第3个图形需要12个小正方形……那么第5个图形中需要小正方形个, 第n个图形中需要小正方形个.
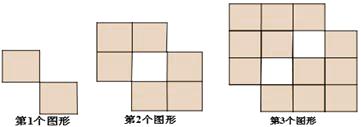
-
科目: 来源: 题型:
查看答案和解析>>【题目】在徒骇河观景堤坝上有一段斜坡,为了方便游客通行,现准备铺上台阶,某施工队测得斜坡上铅锤的两棵树间水平距离AB=4米,斜坡距离BC=4.25米,斜坡总长DE=85米.
(1)求坡角∠D的度数(结果精确到1°)
(2)若这段斜坡用厚度为15cm的长方体台阶来铺,需要铺几级台阶?(最后一个高不足15cm时,按一个台阶计算)
(参考数据:cos20°≈0.94,sin20°≈0.34,sin18°≈0.31,cos18°≈0.95)
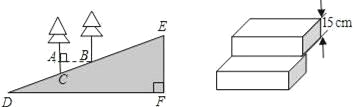
-
科目: 来源: 题型:
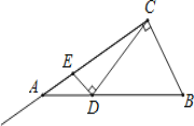
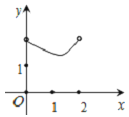
查看答案和解析>>【题目】如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )
A.
 B.
B. 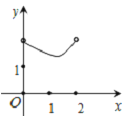 C.
C.  D.
D. 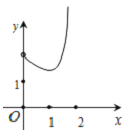
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=2,an=8,则am+n= .
相关试题

