【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=﹣2x+2的图象.

(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.
参考答案:
【答案】(1)A(﹣1,0),(1,0),P(![]() ,
,![]() ).(2)四边形PQOB的面积=
).(2)四边形PQOB的面积= ![]() .
.
【解析】
试题分析:(1)令一次函数y=x+1与一次函数y=﹣2x+2的y=0可分别求出A,B的坐标,再由![]() 可求出点P的坐标;
可求出点P的坐标;
(2)根据四边形PQOB的面积=S△BOM﹣S△QPM即可求解.
解:(1)∵一次函数y=x+1的图象与x轴交于点A,∴A(﹣1,0),
一次函数y=﹣2x+2的图象与x轴交于点B,∴B(1,0),
由![]() ,解得
,解得![]() ,∴P(
,∴P(![]() ,
,![]() ).
).
(2)设直线PA与y轴交于点Q,则Q(0,1),直线PB与y轴交于点M,则M(0,2),
∴四边形PQOB的面积=S△BOM﹣S△QPM=![]() ×1×2﹣
×1×2﹣![]() ×1×
×1×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一内角等于50°,则其它两个内角各为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB是由线段CD平移得到,点A(﹣2,1)的对应点为C(1,1),则点B(3,2)的对应点D的坐标是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2+2(x﹣2)﹣4=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图,
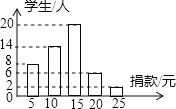
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有800名学生参与捐款,请估计该校学生的捐款总数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
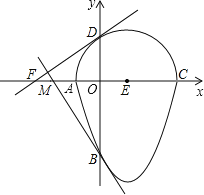
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年12月26日,南昌地铁一号线正式开通试运营.据统计,开通首日全天客流量累积近25万人次,数据25万可用科学记数法表示为( )
A.0.25×105 B.2.5×104 C.25×104 D.2.5×105
相关试题

